Zone d’entraide

GeckoLibre3449

Dans le problème suivant #3 :

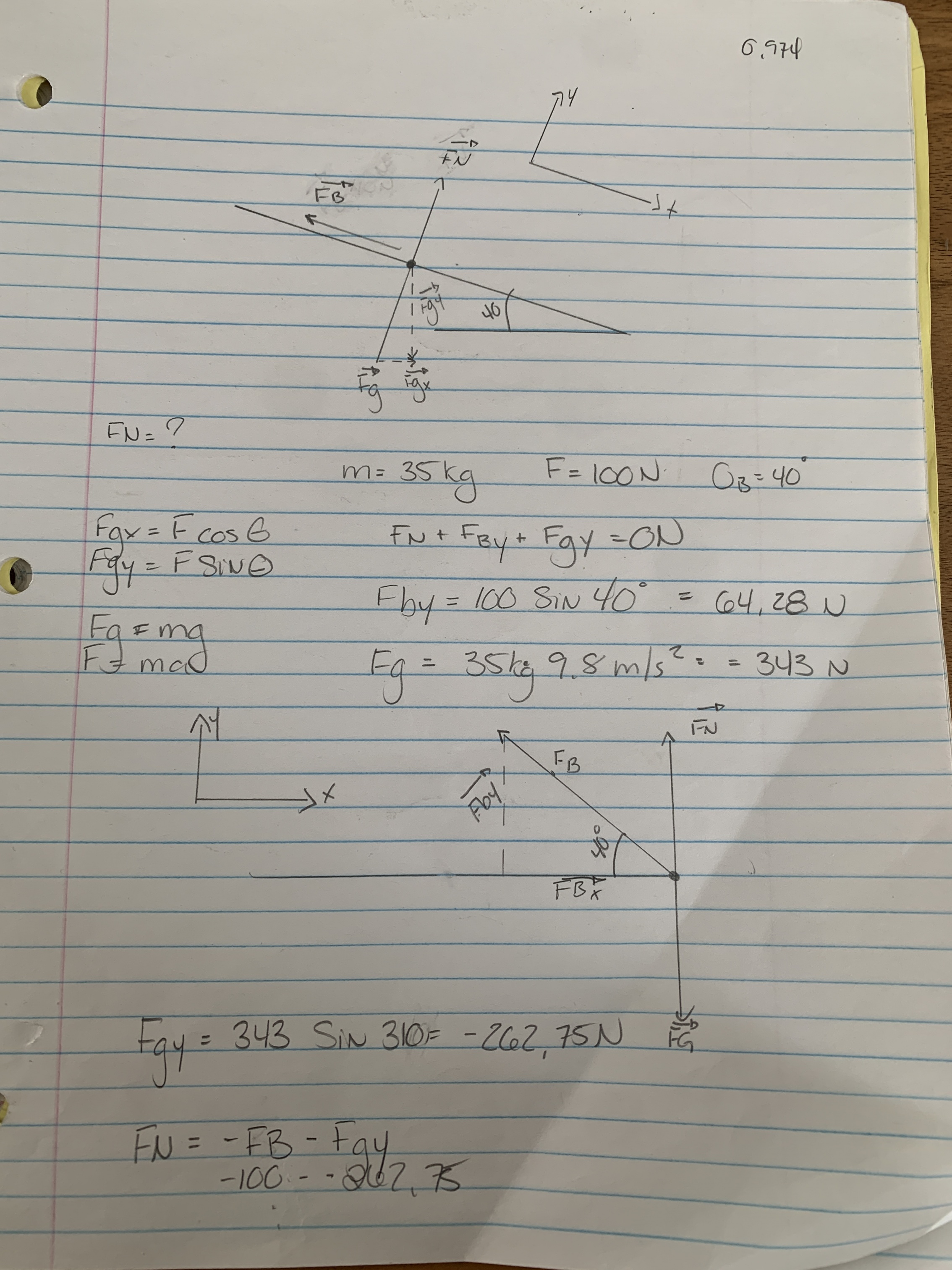
Bernard amène son chien avec lui à la patinoire. Le chien pèse 35 kg er refuse de le suivre et Bernard tire sur sa laisse avec une force de 100N orientée à 40 degrés par rapport à l'horizontale.

Je cherche l'angle de mon Fgy... pour mon équation Fgy=F Sin de? j'arrive à un angle de 310, mais dans le corrigé c'est 270 degré... pkoi?

J'ai déjà posé la question et on m'a référé a la fiche de la force gravitationnelle. J'ai relus et regardé également la mini récup. J'arrive quand même à un angle de 310 degrés au lieu de 270. J'ai reposé la question et on m'a demandé comment je positionnais mon syst.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

de coordonné.

J'ai mis mon système de coordonnées parallèle à la laisse, mais dans le corrigés il semble le mettre parallèle au sol? pourquoi cette préférence? En théorie je devrais tout de même arrivé à la même réponse mais ce n'est pas le cas.

Je vous joins 2 photos en espérant que vous compreniez ma question

Louis-Philippe B

Merci pour ta question!

Effectivement, je pense que le tout se joue dans le système de coordonnées. Il est probablement préférable que le système de coordonnées soit parallèle au sol car cela fait en sorte qu'il faut seulement calculer la composante verticale d'une force.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

En établissant le cadre de référence selon le sol, l'orientation de la force normale devient 90° et celle de la force gravitationnelle devient 270°.

Comme tu l'as bien compris, la somme des forces doit être égale à 0 :

$$ \Sigma_{F_{y}} = 0 = F_N + F_g + F_y $$

Ainsi, tu peux trouver la valeur de la force gravitationnelle et de la composante verticale de la force de la laisse pour trouver la force normale.

Trouvons la force gravitationnelle :

$$ F = mg $$

$$ F = 35 • 9,81 = 343,35\: N $$

Puis, trouvons la composante verticale de la force de la laisse :

$$ F = 100•sin(40°) = 64,28\:N $$

Trouvons la force normale :

$$ \Sigma_{F_{y}} = 0 = F_N + F_g + F_y = F_N+64,28+-343,35 $$

$$ F_N = 279,07 ≈ 279\:N $$

En passant, merci de ta question très bien structurée et qui inclut tes tentatives de démarche ;)

Voilà!