Postsecondaire • 2m
Bonjour!!
Je ne comprends pas comment la réponse donne « continue sur [-3,-1[ U ]2, infini[»
J’ai compris que x ne pouvait pas être égal à -1 et 2, mais je suis perdue par la suite. C’est pour la question 21. Merci!

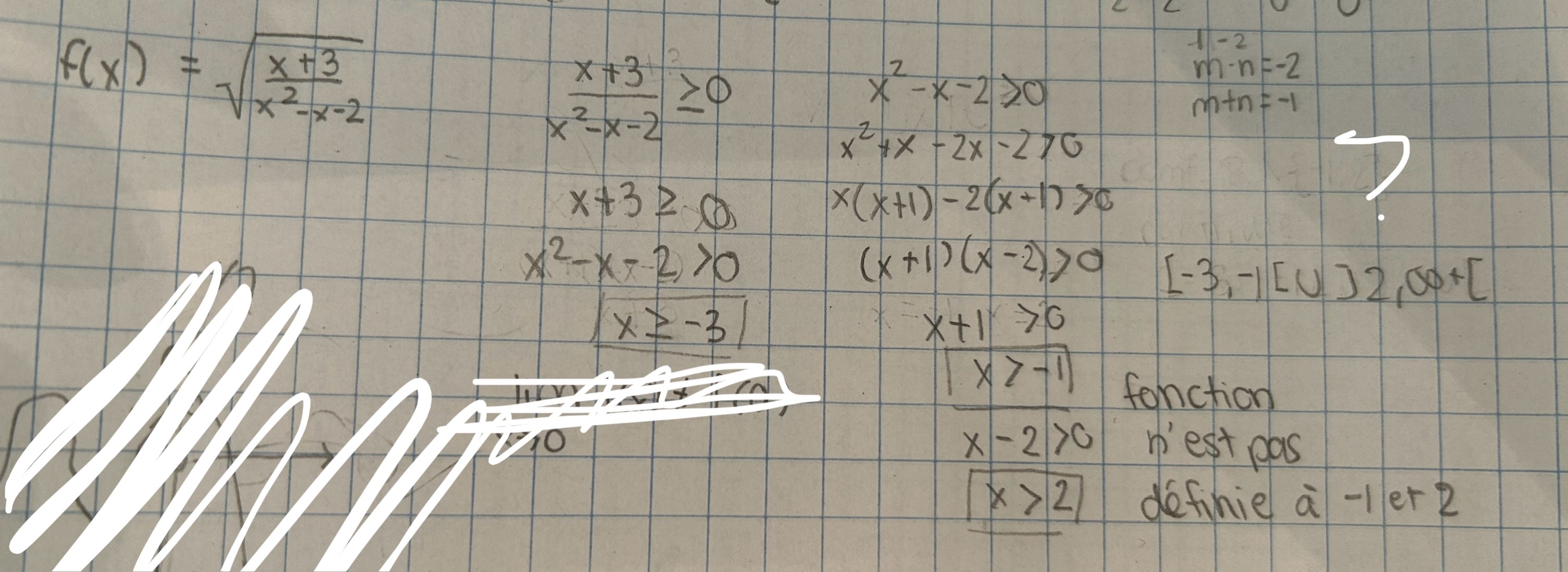






Au numérateur on doIt avoIr x≥-3 pour éviter un nombre négatif.
Au dénominateur tu ne peux avoIr de 0 donc les zéros de la parabole sont exclus x ≠ -1 et x ≠ 2
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Mais la parabole est négative sur tout l'intervalle ]-1,2[ où le numérateur est positif
=> pour éviter d'avoIr la racine carrée d'un nombre négatif: x doIt être dans [-3,-1[ ou ]2,∞
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour ElfeTimide5414,
Merci pour ta question :)
Tu as bien commencé en trouvant la première restriction, c'est-à-dire celle où le dénominateur ne peut être égal à zéro (donc x ne peut être égal à -1 et 2). La seconde restriction provient de la racine carrée. En effet, l'expression à l'intérieur ne peut être négative si on veut qu'elle fasse partie du domaine des réels.
Tu as aussi commencé les bons calculs lorsque tu as fait x+3>=0 et x ^2-x-2>0. Ça nous permet de voir lorsque chacune des fonctions fonction est positive. On peut donc voir que x+3 est positive lorsqu'elle est plus grande ou égale à -3. Pour le dénominateur, on peut calculer que la fonction est négative entre -1 et 2. Donc entre -1 et 2, le numérateur serait positif, mais le dénominateur serait négatif. Le résultat serait donc un négatif dans une racine carrée, ce qui est impossible.
J'espère que cela répond à ta question :)
Sandrine
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!