Zone d’entraide

Sams

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

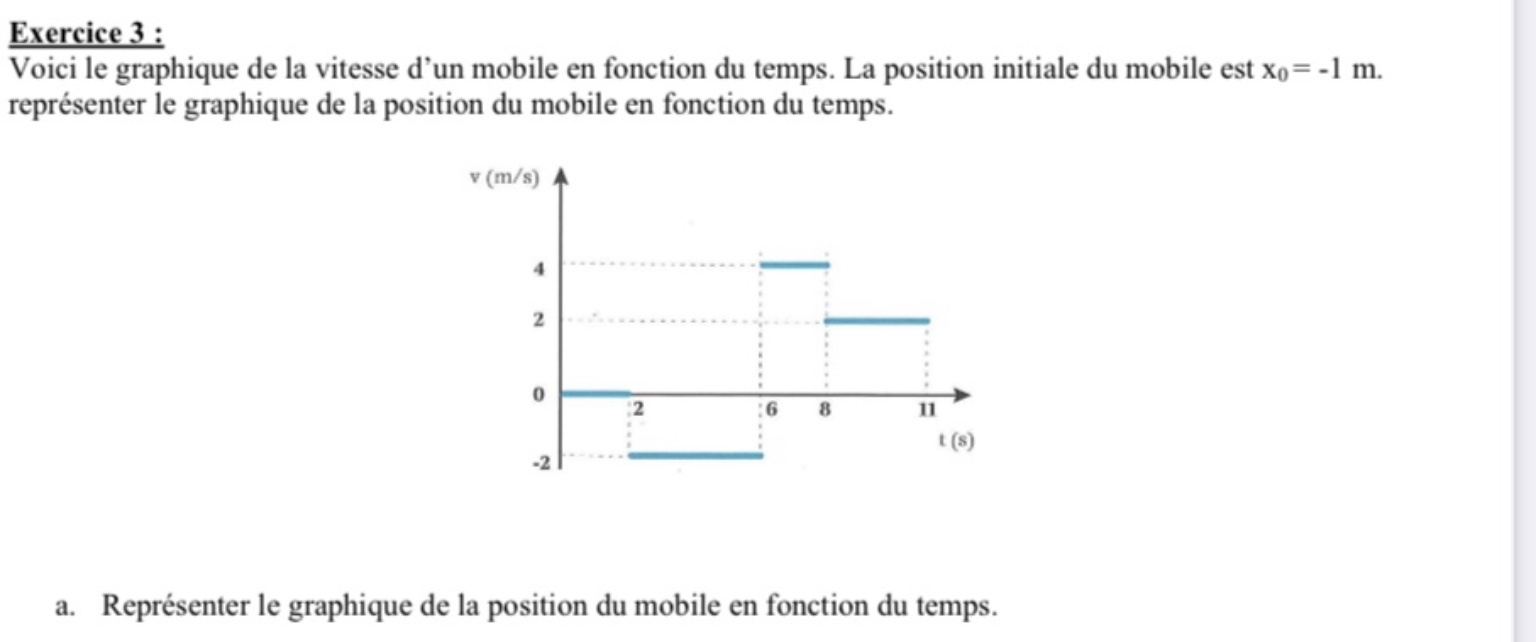
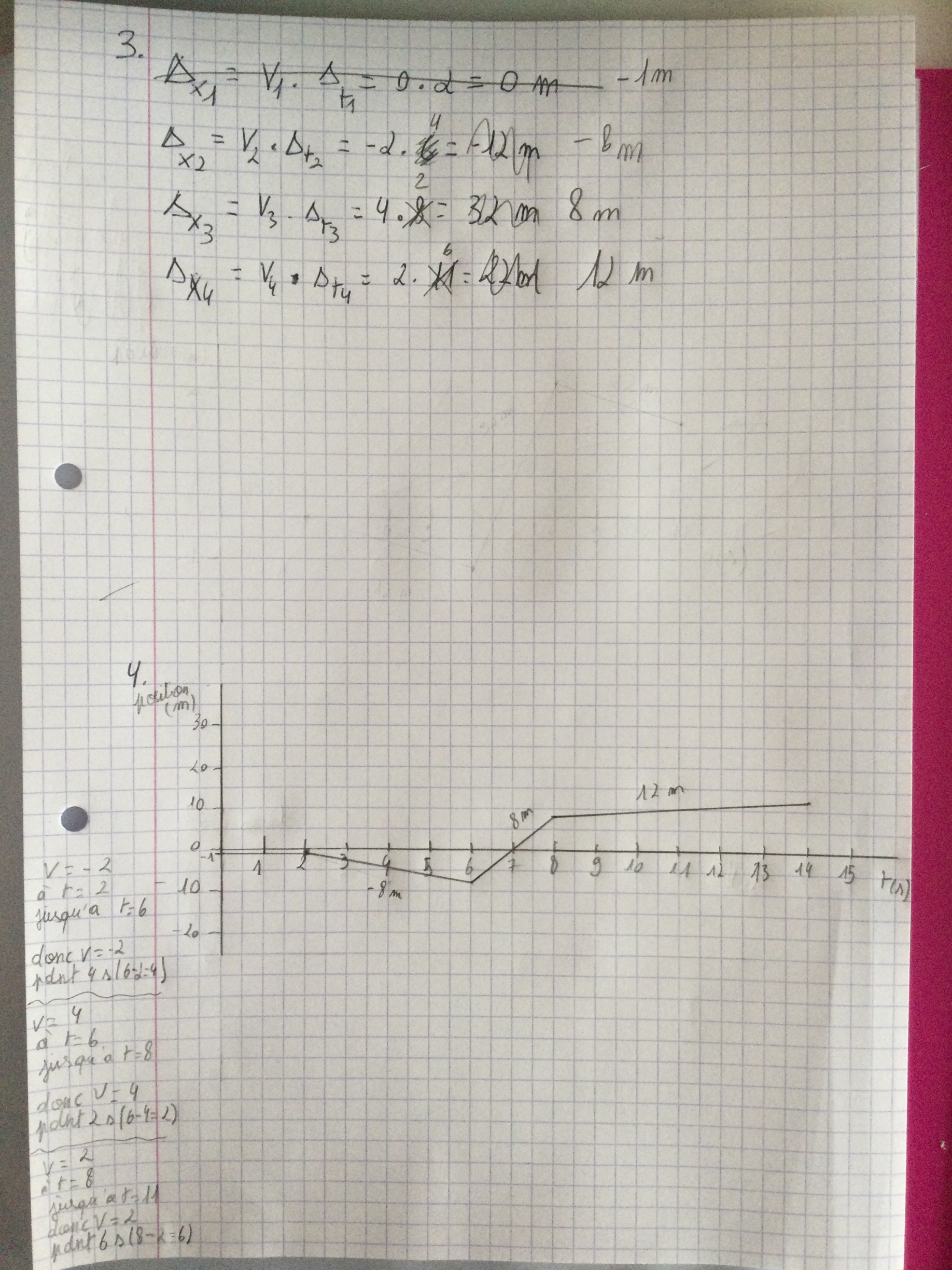
Bonjour j’avais déjà poser la question : « Est ce que mon graphique est correct? » et j’ai essayer de le corriger avec la réponse que j’ai eu et là j’aimerais savoir s’il est correct.

Anthony B

Salut Sams,

Merci pour ta question!

Il y a eu de l'amélioration par rapport à ton graphique précédent, cependant il reste quelques erreurs. Tu as bien débuté cette fois-ci, le mobile débute à -1 m et il n'a aucune vitesse durant 2 s. Ensuite, si tu utilises la formule de la vitesse : V = Δx/ Δt, tu peux trouver le déplacement de ton mobile pour un moment particulier.

Tu as bien fait avec la première vitesse, si on multiplie -2m/s avec 4 s on arrive à un déplacement de -8 m, comme tu l'as identifié. Il est alors à une position de -9 m puisqu'au départ il était à -1 m. Si on regarde la deuxième vitesse, le mobile a une vitesse de 4 m/s durant 2 s, si on applique la formule on trouve un Δx = 8 m. Tu as bien trouvé cette valeur, mais tu l'as interprétée de la mauvaise manière. La position du mobile était à -9 m, s'il se déplace de 8 m, il est rendu à - 1 m et non à 8 m comme tu l'as identifié. Il y a une distinction à faire entre le Δx que tu obtiens à chacun de tes calculs et la position de l'objet en fonction du temps.

Maintenant, je t'invite à ajuster et compléter ton graphique à l'aide de ces informations. Le mobile est à une position de -1 m après 8 s, sa vitesse devient 2 m/s durant 3 s. Je t'invite à trouver son déplacement pour cette période et finalement déterminer sa position finale!

Voici une fiche sur la vitesse si tu veux davantage d'information à ce sujet :

Alloprof aide aux devoirs | Alloprof

https://www.alloprof.qc.ca/fr/eleves/bv/physique/la-vitesse-p1081

Grâce à ses services d’accompagnement gratuits et stimulants, Alloprof engage les élèves et leurs parents dans la réussite éducative.

J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!😉

Anthony B.