Zone d’entraide

SoleilJaune5258

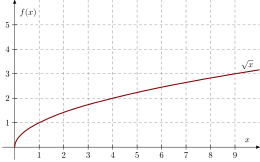
D'accord, merci Mélissa de votre réponse. Toutefois, pourquoi la fonction racine carrée est-elle tournée vers le bas, sachant que plus la hauteur est élevée, plus la portée est grande à son tour? En effet, je dois expliquer si la hauteur a une incidence sur la portée en mettant ces deux variables dans un graphique avec des données expérimentales que j'ai auparavant effectué lors d'un laboratoire. Le contexte c'est le saut d'une personne qui saute d'un immeuble à un autre, donc est-ce comme un projectile horizontal? Pour le moment, mon graphique avait cette allure, mais peut-être me suis-je trompée...

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Kylan T

Bonjour SoleilJaune,

Merci pour ta question!

Si je comprends bien, tu te demandes quel type de fonction va représenter la portée d'un objet selon la hauteur. Par hauteur, veux-tu dire l'angle de projection d'un projectile lancé obliquement, et donc la hauteur maximale qu'il va atteindre (comme sur cette image)?

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ou bien fais-tu plutôt référence à la hauteur d'un objet lancé horizontalement, comme sur l'image ci-dessous?

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Dans tous les cas, la fonction n'aura pas la forme d'une fonction racine carrée. Dans le premier cas (projectile lancé obliquement), la portée maximale du projectile est atteinte lorsque le projectile est lancé à 45°. La fonction ressemblera donc davantage à une parabole: un faible angle de lancer (donc faible hauteur) entraîne une faible portée. Plus l'angle augmente, plus la portée augmente, jusqu'à 45°. Après 45°, la portée diminue symétriquement à la première partie de la fonction, ce qui crée une parabole.

Dans le deuxième cas (projectile lancé horizontalement), la fonction devrait ressembler à une droite (plus la hauteur augmente, plus la portée augmente).

N'hésite pas si tu as encore besoin d'aide:)

Kylan