Secondaire 5 • 4a
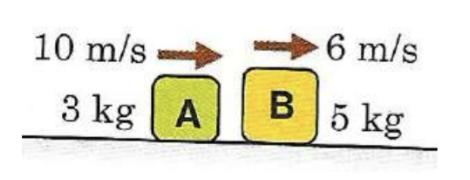
Deux blocs subissent une collision élastique frontale. Immédiatement avant la collision, les deux blocs se déplacent vers la droite: le bloc A (3 kg) se déplace à 10 m/s et le bloc B (5 kg) se déplace à 6 m/s. Calcule les vitesses des blocs immédiatement après la collision (grandeur et orientation).
Réponse: 5 m/s vers la droite; 9 m/s vers la droite






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Puisqu'il y a eu une collision élastique, la quantité de mouvement et l’énergie cinétique ont été conservées, c'est-à-dire que la quantité de mouvement initiale est la même que la quantité de mouvement finale, et l'énergie cinétique initiale est équivalente à l'énergie cinétique finale. Ainsi, pour résoudre ce problème, tu auras besoin de la formule suivante :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puisque la somme des quantités de mouvement au départ doit être égale aux quantités de mouvement à la fin, tu pourras donc poser l'équation suivante :
$$ p_{A_{i}} + p_{B_{i}}= p_{A_{f}}+ p_{B_{f}}$$
Et ensuite insérer les données connues, soit la masse de chacun des blocs et leur vitesse initiale. Puisqu'il reste 2 inconnues, la vitesse finale du bloc A et la vitesse finale du bloc B, nous avons besoin d'une seconde formule (2 inconnues = 2 équations), soit celle-ci :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puisque l'énergie cinétique au départ doit être égale à l'énergie cinétique à la fin, tu pourras poser la formule suivante :
$$Ek_{A_{i}} + Ek_{B_{i}} = Ek_{A_{f}} + Ek_{B_{f}} $$
Puis, tu pourras insérer les données connues dans cette formule, soit les masses des blocs et les vitesses initiales.
Grâce à ces deux équations, tu seras en mesure de déterminer la vitesse finale de chacun des blocs. À toi de jouer maintenant :)
Voici des fiches sur ces notions qui pourraient t'être utiles :
N'hésite pas si tu as d'autres questions!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!