Secondaire 5 • 4a
Bonjour, comment est-ce que je résoudrais la question suivante?
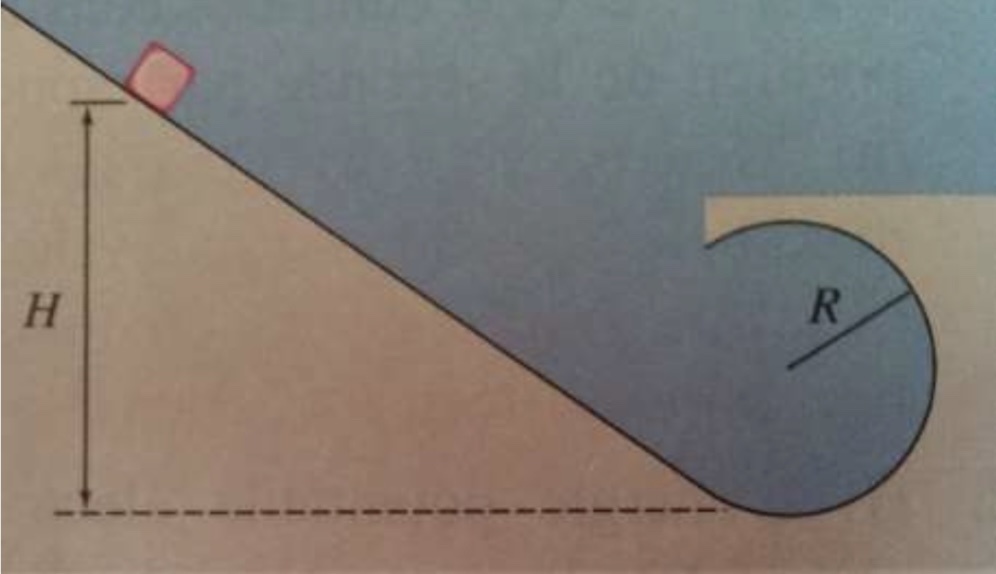
«Un ingénieur chargé de concevoir un manège de parc d'attractions considère une particule de masse m, lâchée d'une hauteur H, qui glisse sur une surface sans frottement se terminant par un cercle. Quelle est sa valeur minimale de H pour que la particule ne par le cercle au point le plus haut du cercle»?
La réponse indique que H min = 5R/2, mais je ne sais pas vraiment quoi faire...






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Merci pour ta question!
Il s'agit d'un problème d'énergie, qui unit énergie potentielle, énergie cinétique et accélération centripète.
D'abord, il est utile de tracer un schéma pour bien représenter les éléments du problème :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ensuite, il faut mettre en relation les différents éléments du problème. En premier lieu, en tout point, l'énergie totale de la particule est égale à la somme de l'énergie potentielle gravitationnelle et l'énergie cinétique, et ce, en vertu de la loi de la conservation de l'énergie (https://www.alloprof.qc.ca/fr/eleves/bv/sciences/la-conservation-de-l-energie-s1090).
$$ E = m•g•y + \frac{1}{2}•m•v^2 $$
Légende :
• E : énergie (J)
• m : masse (kg)
• g : constante d'accélération gravitationnelle (m/s^2)
• y : hauteur (m)
• v : vitesse (m/s)
Sachant que l'énergie est conservée partout où ira la particule, on peut formuler une égalité entre l'énergie de la particule à sa position initiale, et la position de la particule lorsqu'elle est au sommet de la boucle. De cette manière, on pourra trouver la hauteur minimale pour avoir juste assez d'énergie pour franchir la boucle. Il faut noter que y a été remplacé par H pour la position initiale de la particule, et par 2R (le diamètre du cercle) pour la position finale de la particule. La vitesse au point initial est nulle, tel que mentionné dans la question.
$$ m•g•H = m•g•2R + \frac{1}{2}•m•v^2 $$
On constate rapidement que l'on peut mettre m en évidence et l'enlever de l'équation :
$$ g•H = g•2R + \frac{1}{2}•v^2 $$
À ce point, le problème peut sembler arriver à une impasse, considérant qu'aucun facteur ne peut être mis en évidence. Or, en faisant appel à la seconde loi de Newton et aux connaissances de la force centripète et centrifuge (https://www.alloprof.qc.ca/fr/eleves/bv/physique/les-forces-centripete-et-centrifuge-p1020), on trouve que :
$$ \Sigma_F = m•a = F_N+F_g = m•\frac{v^2}{R} $$
Légende :
• m : masse (kg)
• F N : force normale (N)
• F g : force gravitationnelle (N)
• v : vitesse (m/s)
• R : rayon (m)
Note : l'accélération est substituée par v^2/R car il s'agit d'accélération centripète.
Comme il s'agit d'un cas limite et qu'on assume que la vitesse est la vitesse minimale pour franchir la boucle, alors, la force normale exercée par la boucle sur la particule au sommet de la boucle devrait être nulle. Bref, on trouve que :
$$ F_g = m•\frac{v^2}{R} $$
$$ m•g = m•\frac{v^2}{R} $$
$$ v^2=g•R $$
Ceci permet de substituer v^2 dans l'équation initiale par g•R :
$$ g•H = g•2R + \frac{1}{2}•g•R $$
On simplifie alors g :
$$ H = 2R+\frac{1}{2}R $$
$$ H = \frac{5}{2}•R $$
Et voilà!
N'hésite pas si tu as d'autres questions!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!