Zone d’entraide

Olivia

Bonjour,

Voici une question en physique portant sur l'accélération d'un système que je n'arrive pas à résoudre.

Je ne sais pas comment m'y prendre pour écrire l'équation de l'accélération du système suivant en fonction des masses.

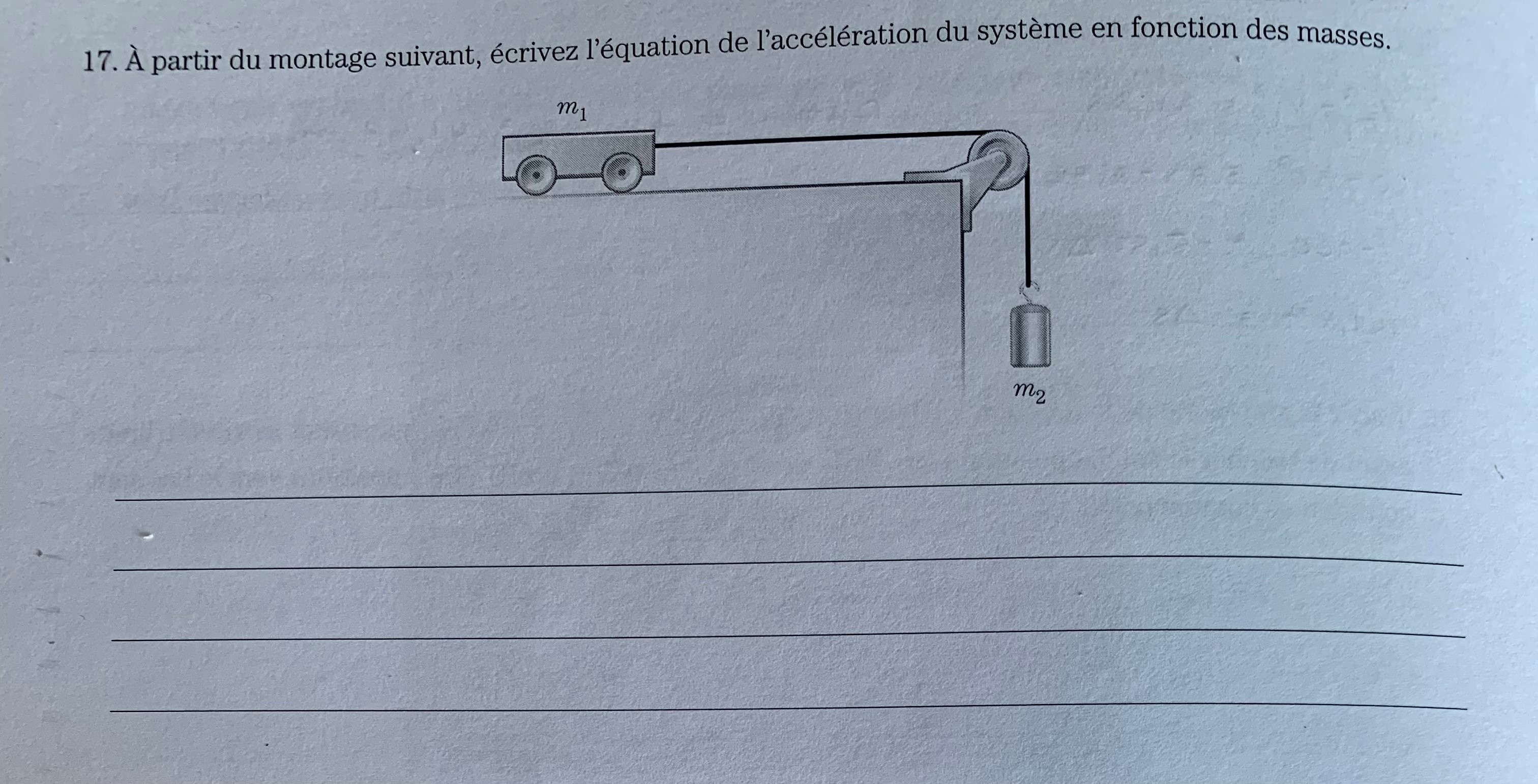
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Louis-Philippe B

Merci pour ta question!

Le problème exige que tu résoudes le tout comme s'il s'agissait d'un problème sans variables. Autrement dit, tu n'as qu'à écrire le problème avec des variables et isoler l'accélération par la suite.

Il faut utiliser la deuxième loi de Newton :

$$ \Sigma_F = m•a $$

Légende :

• Σf = somme des forces sur un axe (N)

• m : masse totale du système (kg)

• a : accélération (m/s^2)

Il faut faire un schéma des forces présentes, afin de pouvoir les additionner dans l'équation :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$$ \Sigma_F = m•a = F_{g\:m_1}+F_N+F_f-F_{g\:m_2} $$

Comme on n'étudie les forces que sur un axe, la force normale et la force gravitationnelle de la masse 1 sont nulles :

$$ \Sigma_F=m•a = F_f-F_{g\:m_2} $$

On peut ensuite développer les expressions pour chaque force :

$$ \Sigma_F = m•a = \mu_c•F_N - m_2•g $$

Puis, on trouve l'expression pour la masse totale, et finalement, l'accélération :

$$\Sigma_F = (m_1+m_2)•a = \mu_c•F_N - m_2•g $$

$$ a = \frac{\mu_c•F_N - m_2•g}{m_1+m_2} $$

N'hésite pas si tu as d'autres questions!