Je ne comorend pas comment résoudre cette question:
une masse de 20 kg est suspendu à 2 ressort identique. Chaque ressort à une constante de rappel de 500 N/m et une masse négligeable.
Quel est l'allongement de chaque ressort
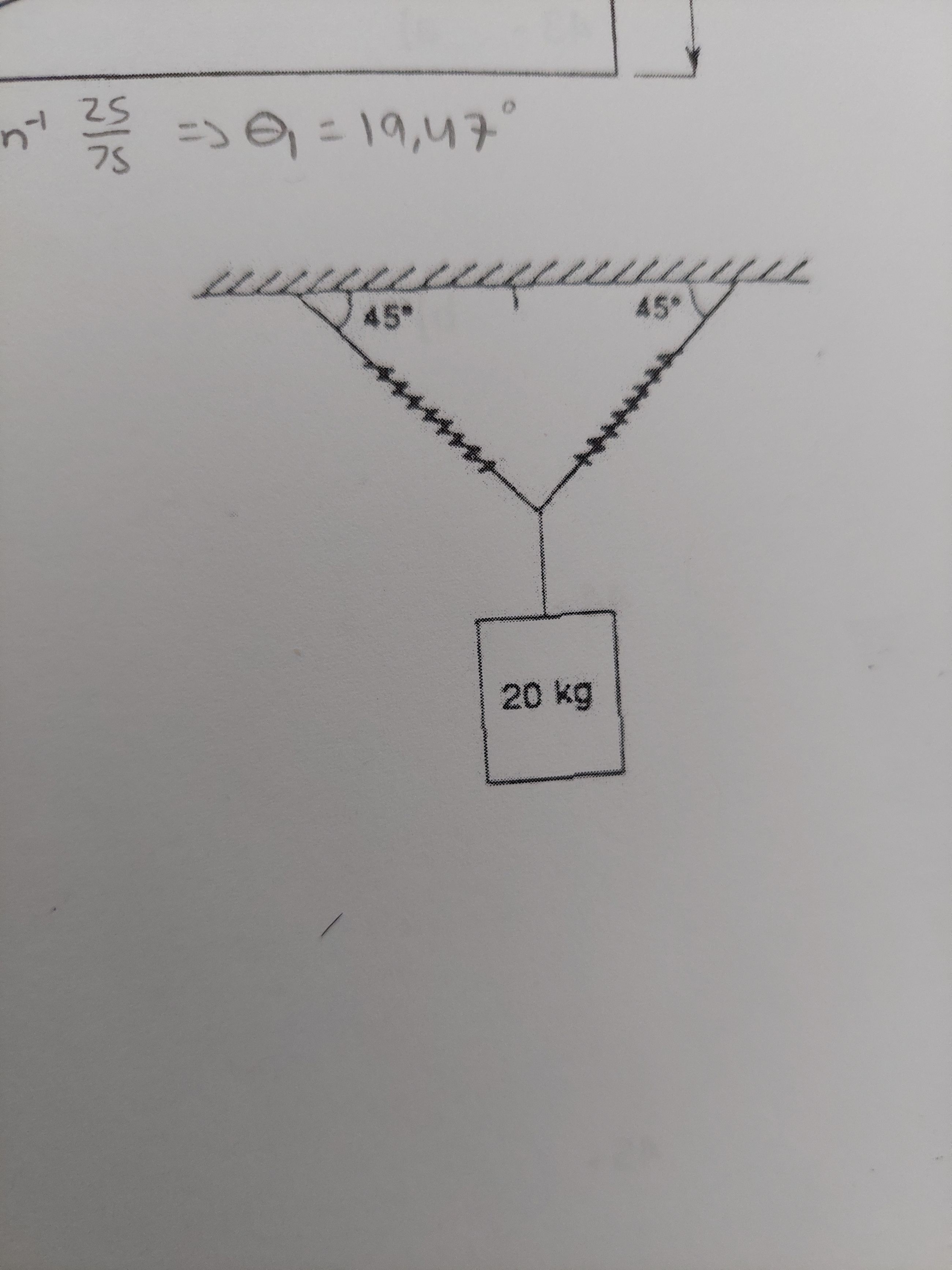
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut Ramneek!
Merci pour ta question.
Pour résoudre ce problème, tu dois utiliser la 2e loi de Newton, qui se résume par l’équation suivante :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puisque le bloc est immobile, l’accélération est donc nulle. Ainsi, la force résultante subit par le bloc est de 0 N. En effet, en voici la preuve :
Fr = m • a;
Fr = m • 0;
Fr = 0.
Le bloc subit plusieurs forces, soit une force gravitationnelle, et deux forces de rappel, exercées par les deux ressorts de masse négligeable. La force gravitationnelle que subit le bloc peux se trouver grâce à la formule suivante :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Sur Terre, l’intensité du champ gravitationnelle est de 9,8 N/kg.
Ainsi, en traduisant la 2e loi de Newton selon l’axe verticale (l’axe des y), nous obtenons l’équation suivante :
Fg - Fr•sin(45°) - Fr•sin(45°)= 0
Puisque les deux ressorts sont placés à 45° de l’horizontale et qu’ils ont la même constante de rappel, le module de leur force de rappel est égal. Pour t’en assurer, tu peux traduire la 2e loi de Newton selon l’axe des x.
Ayant déjà calculé le module de la force gravitationnelle, il ne restera plus qu’à isoler la variable Fr dans l’équation ci-dessus.
Ensuite, en utilisant la formule de la loi de Hooke, soit :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Nous pourrons trouver la mesure de l’allongement des ressorts, soit delta x.
N’hésite pas si tu as d’autres questions! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!