Bonjour quel est la réponse de ces numéros?

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
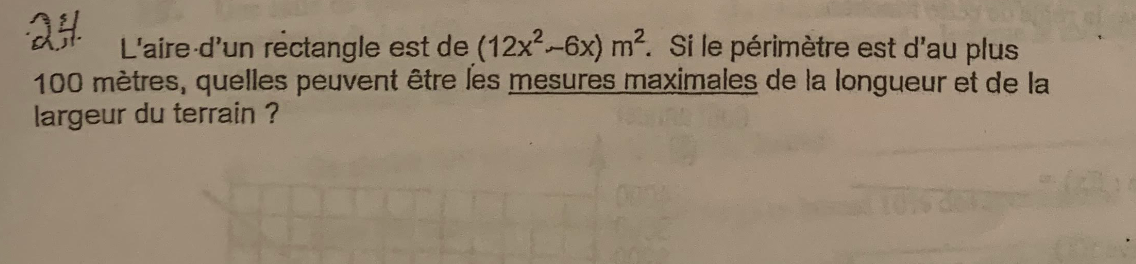
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
bonjour,
#24. Voici ma compréhension du problème:
Aire = 12x²-6x = 6x(2x-1)
Ainsi 6x est la longueur et 2x-1 la largeur (ou le contraire).
On sait que Périmètre \(\leq\) 100
2(6x + 2x-1) \(\leq\) 100
6x + 2x-1 \(\leq\) 50
Je te laisse déterminer la valeur maximale de x et celles de la longueur et de la largeur.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour !
Je vais te faire un meilleur et t'expliquer comment arriver aux réponses 😉
En ce qui concerne le numéro 3, pense à la relation entre \( y \), la seule longeur du rectangle, et plusieurs \( x \), les nombreuses mesures de la largeur. Je te conseille fortement de visiter cette page:
En ce qui concerne le numéro 24, utilise la méthode de comparaison pour le résoudre. On sait que:
$$ A_{rectangle}= L \times l $$ et $$ P_{rectangle}= 2L + 2l $$
Donc,
$$ 12x^{2} - 6x= L \times l $$ et $$ 100= 2L + 2l $$
Avec ces systèmes d'équations, tu seras en mesure de calculer \( L \) et \( l \) .
Consulte cette page pour savoir comment utiliser la méthode de comparaison:
À toi de jouer !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!