Postsecondaire • 4a
La formule que Mr.Thomas avait utilisé pour expliquer à un élève ne me viens pas en tête, quelqu'un pourrait m'aider s'il vous plait car j'aurais un examen bien tôt en mathématiques et le prof a dit qu'il y aurait beaucoup de triangles, il nous permet aussi d'utiliser les formules qu'on veut, même le théorème de Pythagore si on sait l'utiliser.
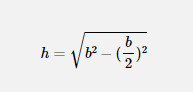






Elle provient du théorème de Pythagore.
On a une cathète b/2, une autre h et l'hypoténuse b, d'où (b/2)²+h² = b² et on isole h.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bien sûr, je vais t'expliquer!
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
En fait, j'ai utilisé le théorème de Pythagore pour remplacer la hauteur dans ce numéro, car on peut trouver la valeur de seulement une variable à la fois, il a donc fallu remplacer la hauteur par son équivalent qui est exprimé avec b comme variable seulement.
C'est dans ce numéro:
Je vais le faire étape par étape pour te montrer, mais c'est un numéro très difficile. (C'est normal d'avoir de la difficulté à voir comment résoudre ce numéro)
Selon le théorème de Pythagore:
$$c^2=a^2+b^2$$
Dans l'image ci-haut, On peut voir b comme l'hypoténuse (c) et a comme la demi-base (b/2) qui forme un triangle rectangle avec b et h (la hauteur). La hauteur (h) sera alors le b du théorème de Pythagore. Si on isole b (du théorème de Pythagore) on obtient cela:
$$b^2=c^2-a^2$$
Et ensuite,
$$b=\sqrt{c^2-a^2}$$
Si on remplace alors a, b et c par les valeurs que nous avons établies dans le paragraphe plus haut, tu retrouves la formule dont tu parles:
$$h=\sqrt{b^2-(\frac{b}{2}})^2$$
Voilà! C'est comme ça que j'ai fait!
C'est un peu mélangeant à cause du b du théorème et du b qui représente la base du triangle, c'était moins mélangeant en utilisant directement le théorème de Pythagore adapté à la situation comme dans mon explication, car j'avais seulement une variable b;) (J'ai mis les a, b et c du théorème en italique dans l'explication)
C'est possible seulement parce que c'est un triangle équilatéral, puisque les 3 côtés sont isométriques.
J'espère que c'est plus clair maintenant!
Bonne soirée!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!