Bonsoir,
J'aurais besoin d'aide avec ce problème : un funambule de 70kg se tient au milieu d'une corde de longueur 100m. Si le centre de la corde s'abaisse de 1,5m, trouvez le module de la tension dans la corde.
Voici ma démarche :
Par la suite, on sait que la somme des forces externes = -vecteurT1 + vecteur T2 - vecteur T3 = 0, d'où la somme des forces en x = T1cos88° - T2cos2°-T3cos270°=0 --> T1cos88° = T2cos2°, d'où T1cos88°/cos2° = T2 = à peu près 0,0349T1.
Nous savons également que la somme des forces en y = T1sin88° + T2sin2° -686 N = 0 --> 0,999 + 0,0349 (0,0349) T1 = 686 N.
Ainsi, après avoir trouvé un T1 de 562394N, j'ai trouvé un T2 de 19628N en substituant T1 dans T2 = 0,0349T1.
Finalement, en remplaçant, ces valeurs, dans un T1cos88°;T1sin88° ainsi que T2cos2°;T2sin2°, je n'obtiens pas une somme des forces en x ainsi qu'une somme des forces en y, comme qu'on devrait étant donné qu'on a utilisé la 1er loi de Newton.
La bonne réponse est de 11,4 x 10^3 N.
En attente d'une réponse, je vous souhaite une bonne soirée! ;)
OrAutonome2754







Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
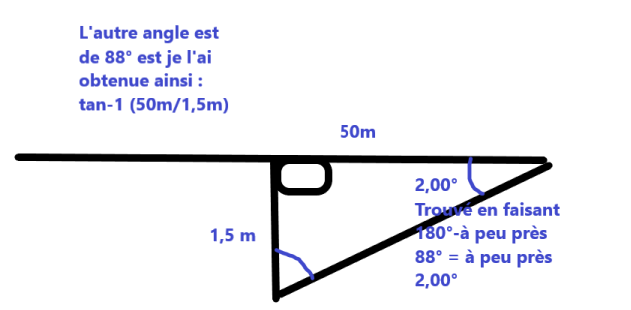
Voici comment je dessinerais le probleme :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puisque c une corde la tension est egale partout donc la norme de T1 = la norme de T2 (Posons T etant la norme de T1 = la norme de T2 pour la suite de l'exemple)
On peut poser l'équation en x = 0
0 = T1cos(2) - T2cos(2)
0 = T cos(2) - T cos (2) = 0
On peut poser en y
0 = T1 sin(2) + T2 sin(2) - T3
0 = T sin(2) + T sin(2) - mg
mg = 2* T * sin(2)
T = mg/(2*sin(2))
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!