Toujours à ton boulot d'été, ton superviseur veut mettre à l'épreuve tes capacités en physique. Un nouveau treuil (un câble entraîné par un moteur) doit servir à hisser des charges sur une rampe inclinée. Ton superviseur s'inquiète que les colis arrivent trop vite en haut de la rampe.
Contraintes
- La rampe inclinée est composée de petits cylindres libres de tourner : il n'y a aucun frottement entre la rampe et la charge.
- L'angle θ
- de la rampe par rapport à l'horizontale est connu.
- Le câble du treuil exerce une force connue.
- Le câble est orienté à un angle α
- par rapport à l'horizontale.
- La charge, initialement immobile, a une masse connue.
- La longueur de la rampe est connue.
Schématisation
Dessine un schéma de l'objet qui nous intéresse. Trace tes axes des x
et des y
. Dessine et nomme chaque force subie par l'objet qui nous intéresse.
Modélisation
Construis un modèle pour calculer la vitesse finale de la charge à son arrivée en haut de la rampe, en fonction des paramètres connus. Teste ensuite ton modèle avec les valeurs suivantes:
L'angle de la rampe : 25
∘
La tension dans le câble : 42N
L'angle du câble par rapport à l'horizontale : 38
∘
La masse de la charge : 2.4kg
La longueur de la rampe : 3.5m
Voici m’a démarché , j’arrive pas à trouver mon erreur
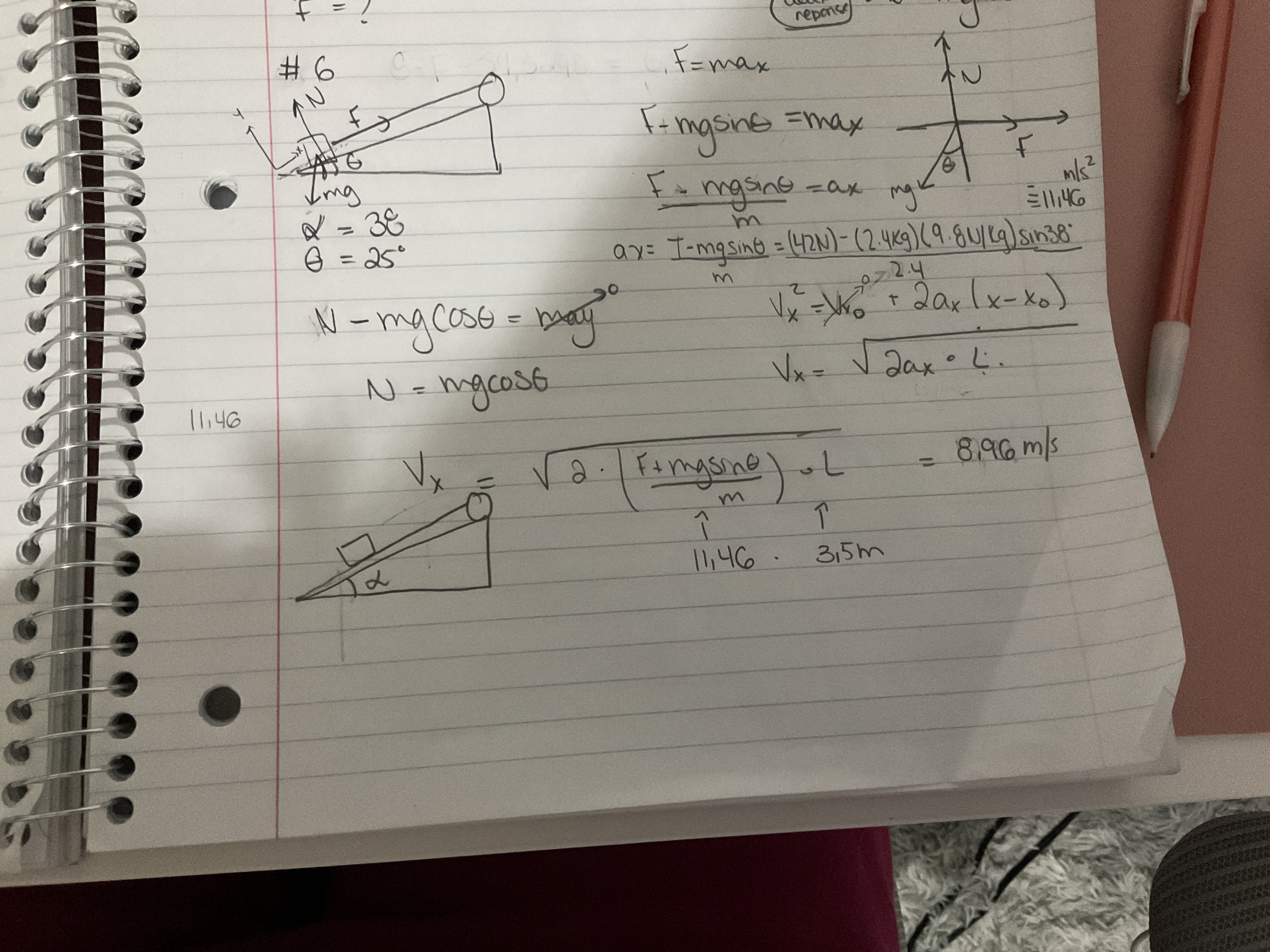
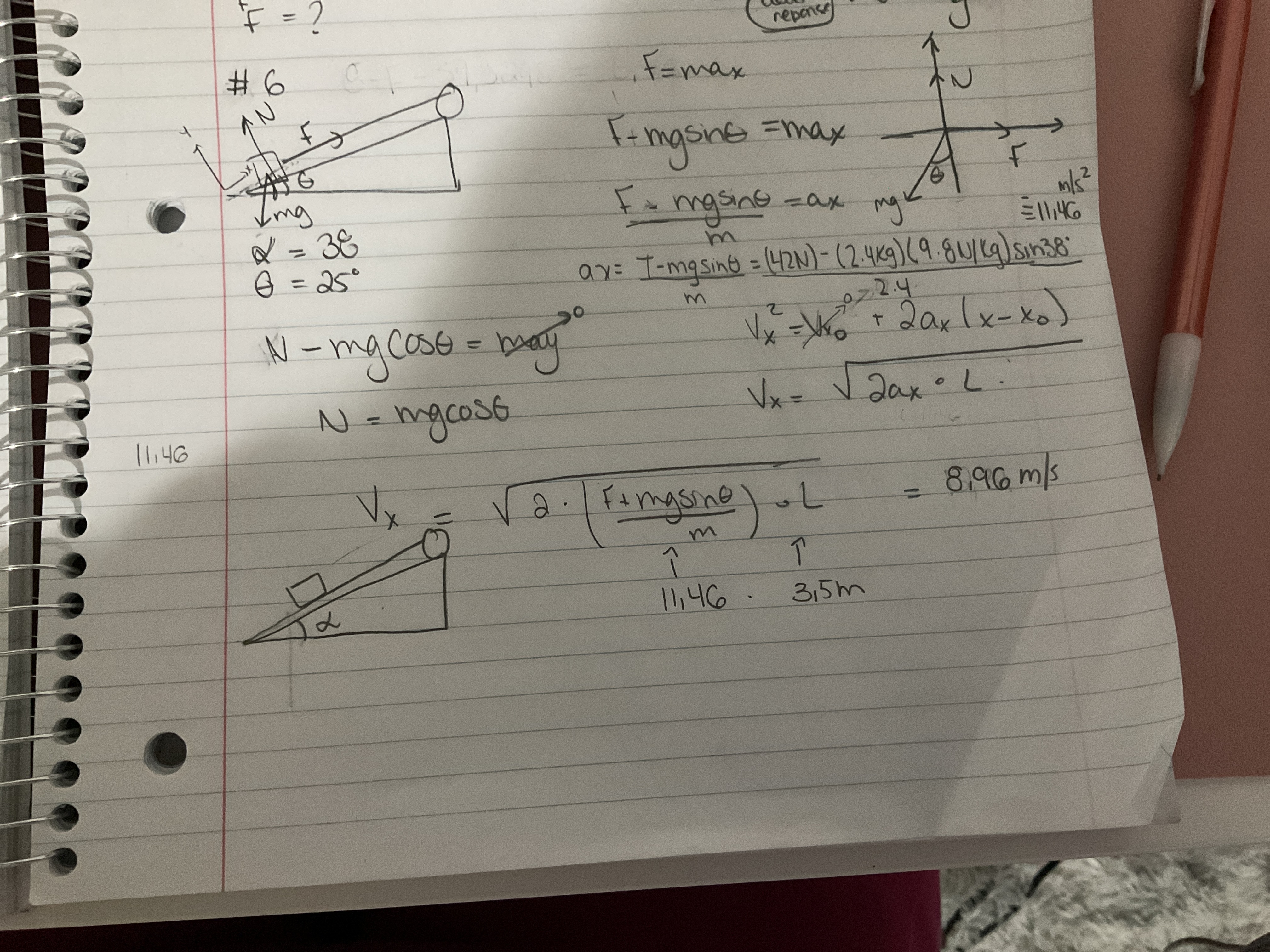






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Merci pour ta question!
Je te suggère d'adopter une démarche différente. D'abord, du peux établir que le plan incliné forme l'axe des x :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puis, tu peux trouver la composante en x de la force gravitationnelle et la composante en x de la tension :
$$ F_{gx} = F_g•cos(270-25°) = mgcos(270-25°) $$
$$ F_{gx} = 2,4•9,81•cos(270-25) = -9,95\:N $$
$$ F_{Tx} = F_T•cos(38-25°) = 42•cos(38-25) = 40,92\:N $$
Ensuite, tu peux trouver l'accélération grâce à la deuxième loi de Newton :
$$ \Sigma_F = ma $$
Légende :
• Ef : somme des forces (N)
• m : masse (kg)
• a : accélération (m/s^2)
$$ \Sigma_F = 40,92-9,95 = (2,4)a $$
$$ a ≈ 12,906\:m/s^2 $$
Grâce à la formule du MRUA, tu peux trouver le temps que prend le bloc à monter la pente :
$$ x_t = x_i+v_i•t+\frac{1}{2}•a•t^2 $$
Légende :
• xt : position horizontale à l’instant t (m)
• xi : position horizontale initiale (m)
• vi : vitesse horizontale initiale (m/s)
• t : temps (s)
• a : accélération (m/s^2)
$$ 3,5 = 0+0t+\frac{1}{2}•12,906•t^2 $$
$$ t ≈ 0,736\:s $$
Finalement, tu peux trouver la vitesse de la masse grâce à la formule de la vitesse selon le temps :
$$ v_t = v_i+a•t $$
Légende :
• vt : vitesse à l’instant t (m)
• vi : vitesse initiale (m)
• a : accélération (m/s^2)
• t : temps (s)
$$ v_t = 0 + 12,906•0,736 ≈ 9,50\:m/s $$
Voilà!
Cette fiche du site d'Alloprof explique la deuxième loi de Newton :
N'hésite pas si tu as d'autres questions!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!