Primaire 6 • 3a
Bonjour, pour la réso suivante:
Dans un sac, il y a 7 bonbons
- 2 rouges
- 1 vert
- 3 mauves
- 1 bleu
Ismael a le droit de piger deux bonbons. Quelles sont les possibilités de combinaisons de bonbons ? Dessine l’arbre des probabilités. Combien y a-t-il de possibilités ?
Quelles sont les probabilités qu’il ait deux bonbons bleus ?
Quelles sont les probabilités qu’il ait deux bonbons de la même couleur ?
Quelles sont les probabilités d’avoir deux bonbons mauves ?
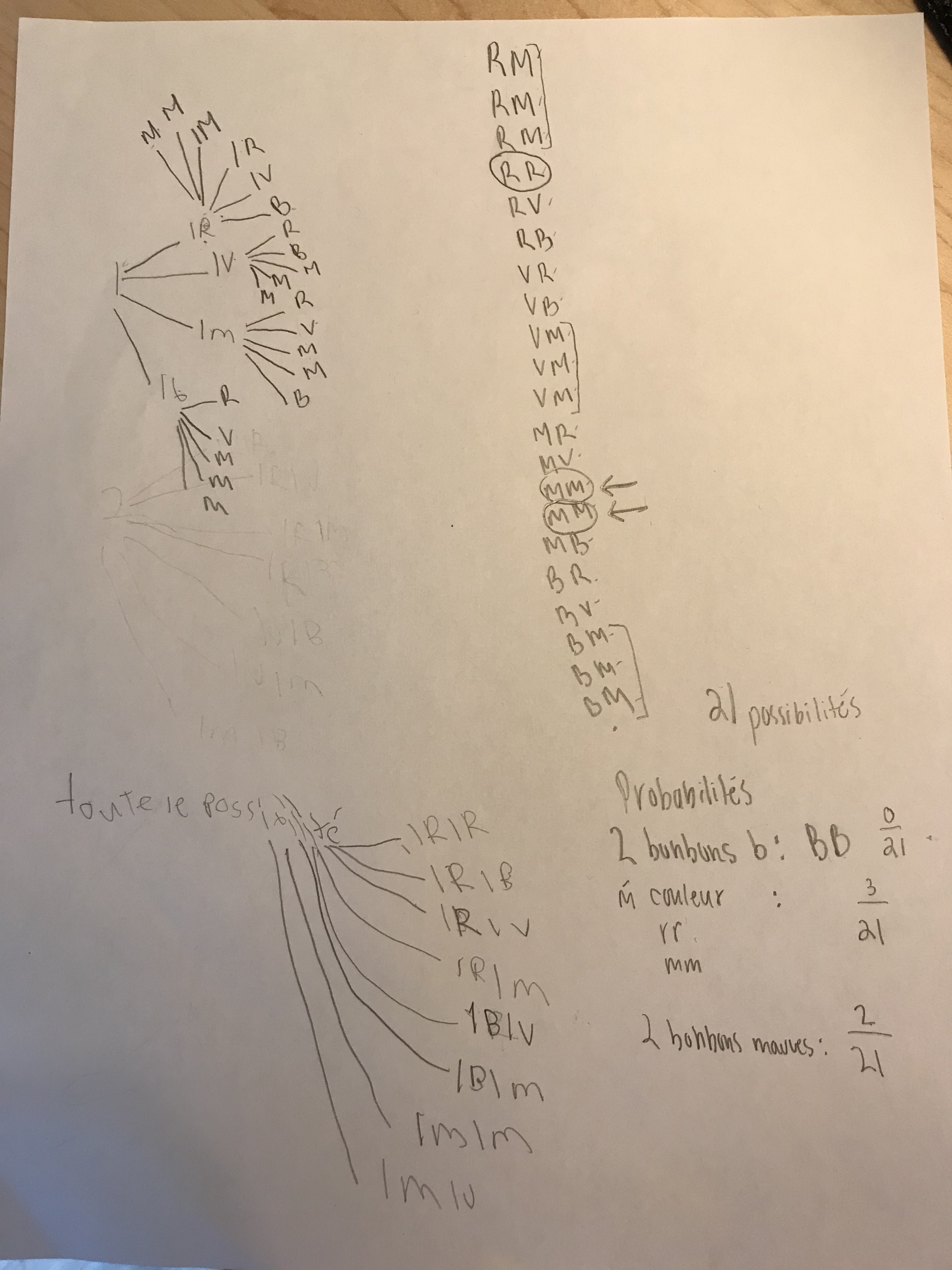
Est-ce que je dois calculer le mauve de cette façon dans cet arbre de facteurs? Je me questionne s'il y a bien 21 possibilités? ou le RM compte pour 1 possibilité dans l'univers des possibles?
Merci






bonjour,
On pourrait dessiner seulement les branches qui sont dans la question:
• P(deux bonbons bleus) = ?
----- 1/7 ------ B ----- ?/6 -------- B
Note: Il n'y a qu'un seul bonbon bleu.
• P(deux bonbons de la même couleur)
----- 2/7 ------ R ----- ?/6 -------- R
----- 3/7 ------ M ----- ?/6 -------- M
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Bonjour Mayson en faite, quand tu fais ton arbre, à la première étape, il faut que tu mettes toutes les combinaisons
En faite, toi tu as mit à ton étape 1 que chaque branche c'est 1R , 1B, 1M, 1V . Cependant, cela n'est pas vrai, car il n'a pas 1 chance sur 4 de piger une couleur. Il a plus de chance de piger un mauve qu'un rouge par exemple, donc tu dois respecter cela
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Regarde, la 1er fois qu'il pige, il a 2 chances sur 7 de piger un rouge, 1/7 un vert, 3/7 un mauve, 1/7 un bleu. Ensuite, une fois que tu as fait les premières branches, il faut passer aux deuxièmes branches , donc la deuxième fois qu'on pige !. Rappel toi que si il a pigé un rouge le 1er fois, bien à la deuxième pige, il ne peut piger qu'un seul rouge (car le 1er rouge est déjà partit à la première pige) . Donc il aurait 1/6 de piger un rouge, 1/6 un vert, 3/6 un mauve et 1/6 un bleu. Ainsi , juste avec les 2 branches que j'ai fais (étape 1 et 2) nous avons les combinaisons suivantes ; RR-RV-RM-RB.
Pour répondre à ta question ; Quelles sont les possibilités de combinaisons de bonbon ; on parle ici juste des possibilités , donc RR-RM-RV etc, tu ne vas pas répéter plusieurs fois RM , car RM est une combinaison même s'il y plus de probabilités d'avoir RM que RR par exemple. Il y a donc moins de 21 combinaisons possibles (RM compte RM juste 1 fois) , mais il y a plus de probabilités d'avoir RM que RR, voila la nuance !
Voici un lien Alloprof sur les probabilités
Cordialement, VC
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!