Zone d’entraide

OrnithorynqueChouette3758

Bonjour, je ne comprends pas quand le h est + ou -?

Voici dans cet exemple:

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

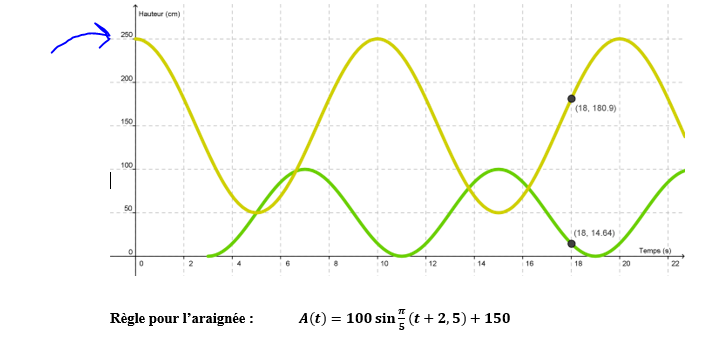
La règle correspond la fonction sinus en jaune. Je ne comprends pas pourquoi le h est + 2,5 et non -2,5? Est-ce que le h pourrait être autre chose comme -7,5?

Simon

Salut Isabel,

deux choses. D'abord oui, il y a une infinité de fonctions sinusoïdales qui ont la même représentation graphique. Si tu trouves une valeur de \(h\) possible, en ajoutant ou soustrayant un multiple de la période, tu peux trouver autant d'autres valeurs de \(h\). De plus, si tu es prête à changer les signes de \(a\) ou \(b\), tu peux trouver encore d'autres valeurs de \(h\) possibles (en ajoutant ensuite un multiple d'une demi-période). Habituellement, on prend la valeur de \(h\) la plus près de l'axe des \(y\) ; cela dit, ce n'est pas parce que tu n'as pas la « réponse » du corrigé que la tienne n'est pas correcte.

Ensuite, dans \[f(x) = a\sin\left(b\left(x-h\right)\right) + k\]la forme canonique de la fonction sinus, c'est bien \(x - h\) avec un « moins » entre \(x\) et \(h\). Ainsi, si tu as \[f(x) = a\sin\left(b\left(x + 2,\!5\right)\right) + k\]la valeur de \(h\) n'est pas \(+2,\!5\) mais bien \(-2,\!5\) car \[f(x) = a\sin\left(b\left(\textcolor{Red}{x+2,\!5}\right)\right) + k\] est en réalité \[f(x) = a\sin\left(b\left(\textcolor{Red}{x - (-2,\!5)}\right)\right)\]Ainsi, la règle donnée me semble bonne et \(h = -2,\!5\) comme tu l'avais déduit.

N'hésite pas à nous réécrire au besoin :-)