Secondaire 5 • 3a
Bonjour, pour les question j'ai réussi à avoir la première ligne des réponses possible mais je ne comprends pas comment ils ont arrivé à trouvé ceux en deuxième ou troisième.
C'est-à-dire, pour le b) je sais que le 6n est la période mais est-elle seul comme le premier cycle commence sur l'axe des ordonnée? Je ne suis pas tout à fait sûre pourquoi le 6n est tout seul et pourquoi après on ajoute 3?
pour le c), pourquoi on ajoute 2 et ensuite on ajoute 4?
Merci
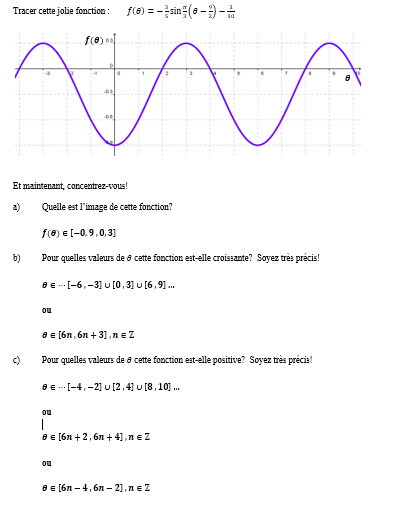






La période est 6.
Tu prends un des intervalles sur la première ligne et tu ajoutes n fois la période aux bornes de l'intervalle:
b) [0+6n, 3+6n]
c) [2+6n, 4+6n]
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour OrnithorynqueChouette3758,
Merci d'utiliser la zone d'entraide.
Ici, la fonction en question est celle de sinus.
En ce qui concerne la lettre b, dans cette fonction respective, le a et b sont de signes contraires. Ce qui signifie que la fonction sera croissante sur l'intervalle:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
En ce qui concerne la lettre c, une fonction est positive sur un intervalle donné en x si, sur cet intervalle, les valeurs de f(x) sont supérieures ou égales à 0 (positives). Les intervalles où la fonction est positive dépend des zéros de la fonction (Ce sont les valeurs de x pour lesquelles f(x)=0), de la période et de l'allure du graphique. Tu peux trouver tout simplement les x, comme indiqué, ou calculer que la fonction est positive sur les intervalles de la forme:
〚 1er zéro de la fonction + n ; 2ème zéro + n 〛
Pour en savoir plus à ce sujet, consulte la fiche Les propriétés de la fonction sinus (cosinus) | Alloprof .
Je te laisse prendre connaissance de tout cela et n'hésite pas à nous écrire de nouveau pour plus de précisions.
Laura
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!
Fiche
Les chaines et les cycles chaîne cycle Euler Hamilton arête sommet cycle eulérien cycle hamiltonien chaîne hamiltonienne chaine et cycle hamiltonien graphe connexe Les chaines et les cycles | Secondair...
| Secondaire 5