Zone d’entraide

RorqualCocasse6516

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Bonjour!

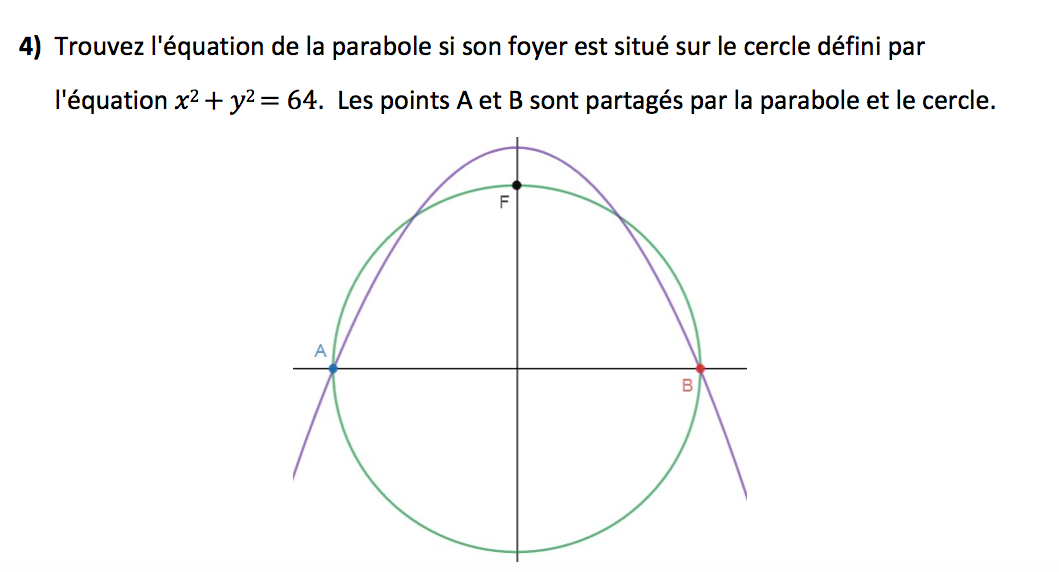
Je dois trouver l'équation de la parabole. Pour cela j'ai besoin du sommet ainsi que la valeur «c» de la parabole. J'ai déjà pu trouver les coordonnées du foyer, du point a et du point b grâce à l'équation du cercle. F(0,8), A(-8,0), B (8,0). Mais même avec ces informations je ne trouve pas le sommet (0,k) Merci!

Simon

Salut,

Je me permets de faire du pouce sur la réponse d'Alain...

L'équation de la parabole est \[(x-h)^2 = 4c(y - k)\]En remplaçant ce qu'on connaît, \(h =0\), on obtient

\[x^2 = 4c(y - k)\]

On connaît aussi les coordonnées du foyer, mais pas de la valeur de \(c\) (soit la distance signée entre le foyer et le sommet de la parabole). Note qu'ici, \(c\) est négatif car la parabole est ouverte vers le bas. Cela nous permet d'écrire \[k = 8 - c\]tu vois pourquoi ?

On remplace ensuite \(x\) et \(y\) par \((8, 0)\) \[8^2 = 4c(0 - k)\] \[64 = 4c(-k)\] \[64 = -4ck\]On peut diviser par \(-4\) pour simplifier un peu \[-16 = ck\]et on substitue \(k\) par \(8-c\) \[-16 = c(8-c)\]Résous ensuite \[-16 = 8c - c^2\] \[c^2 - 8c - 16 = 0\]en complétant le carré ou avec la formule quadratique. J'obtiens aussi une valeur irrationnelle comme Alain (l'équation a deux solutions, une positive et une négative, mais on ne conserve que la négative). Tu peux ensuite calculer la valeur de \(k\) facilement car \[k = 8 - c\]

AvocatTenace6777

bonjour,

Consulte cette fiche:

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-parabole-conique-m1330

On y trouve l'équation de la parabole verticale transformée et les coordonnées du foyer en fonction de k et c.

On cherche la valeur de c et de k.

Tu devras utiliser un point sur la parabole par exemple le point (8,0) et les coordonnées du foyer (0,8) pour écrire et résoudre deux équations où les variables sont c et k.

J'obtiens deux nombres irrationnels.