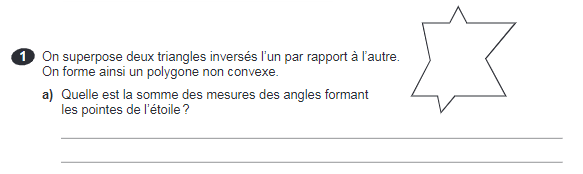
Secondaire 1 • 3a
Bonjour je voudrais savoir comment peut-on trouver la réponse de cette question, car je ne comprends pas comment y répondre, pouvez-vous me donner des indications afin que je puisse trouver la réponse moi-même, aussi je voudrais savoir la formule pour trouver les angles rentrant dans ce polygone convexe! Merci beaucoup au prof qui me répondra :) !






Salut,
Consulte bien l'explication de Katia pour répondre à la question.
Pour ce qui est de la somme de tous les angles, incluant les angles rentrants, ça fonctionne un peu comme avec les polygones convexes. Pour trouver la sommes des angles intérieurs, habituellement, dans un polygone convexe, on choisit un sommet et on trace toutes les diagonales pour former des triangles. Il y a toujours deux triangles de moins qu'il y a de côtés. C'est pourquoi tu as peut-être vu la formule \[\text{Somme} = (n-2)\times 180^{\circ}\]
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour un polygone concave, étonnament, ça fonctionne aussi ! Il faut cependant choisir plus d'un sommet. Dans ton cas, par exemple :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Il y a 10 triangles (le polygone concave initial a douze côtés et 12 - 2 = 10). Tous les angles des triangles forment les angles du dodécagone.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
La somme des mesures des angles intérieurs d'un triangle est toujours de 180 degrés. Ainsi, sachant que ce polygone est formé de 2 triangles, et que chaque pointe de l'étoile est la pointe d'un triangle, tu peux donc trouver la somme des mesures des angles formant les pointes de l'étoile.
Il n'y a pas de formule pour trouver la somme des mesures des angles intérieurs de ce polygone. Cependant, voici un tableau illustrant la somme des mesures des angles intérieurs de différentes formes, ce qui pourrait t'être grandement utile pour résoudre de futurs problèmes similaires à celui-ci :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
N'hésite pas si tu as d'autres questions :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!