Secondaire 5 • 3a
Bonjour, pouvez-vous m'expliquer en détail ce qu'ils ont fait pour trouver l'angle. Je croyais la réponse était seulement 52.27°.
EDIT: Merci :), il faut trouver l'orientation puis moi justement je ne comprends pas comment faire, pouvez-vous expliqué justement le à partie de «puis»?

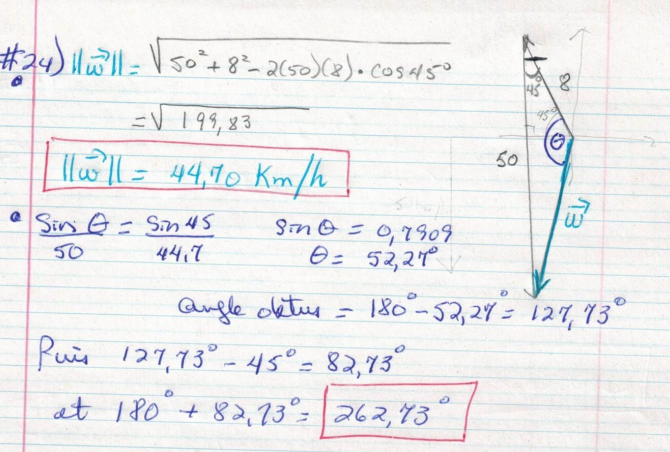






Pour t'aider à trouver l'orientation,
envoie une image de l'énoncé complet de la question.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut Nath777!
Pour résoudre ce problème, ton professeur a d'abord calculé la norme du vecteur \( \overrightarrow{w} \).
Ensuite, il a utilisé la loi des sinus pour déterminer l'angle \(\theta\). En utilisant simplement la fonction \(\sin^-1\), on a:
$$ \theta = \sin^{-1} (\frac{50 \sin(45°)}{44,7} ) = 52.27 ° $$
Par contre, on cherche l'angle qui est plus grand que 90°. On doit donc trouver son angle supplémentaire avec:
$$ 180° - 52.27° = 127.73°$$
Pour s'en convaincre, on peut calculer l'autre angle inconnu du triangle avec la loi des sinus:
$$ \frac{8}{\sin \phi} = \frac{44.7}{\sin (45°)} $$
On trouve \( \phi = 7.27°\). Comme on sait que la somme des angles d'un triangle est 180°, on trouve donc \( \theta\) avec:
$$ \theta = 180° - 45° - 7.27° = 127.73° $$
Pour les deux dernières lignes, je ne sais pas précisément pourquoi ton professeur a fait cette démarche. Je crois qu'avec l'énoncé je pourrais mieux t'aider.
Charles
bonjour,
C'est parce que si l'angle \(\theta\) est obtus alors il faut prendre le supplémentaire de 52.27°.
Et cela est possible parce que sin(\(\theta\)) = sin(\(\pi-\theta\)).
Pour le reste, il faudrait l'énoncé de la question.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!