Secondaire 5 • 3a
J'ai souvent de la misère avec les démonstrations, plus particulièrement celles des identités trigonométriques. Avez-vous des suggestions à me donner pour réussir? Par exemple, les étapes de raisonnement et d'autres conseils.
Pouvez-vous m'aider à l'aide de cet exemple?
Je vous remercie.
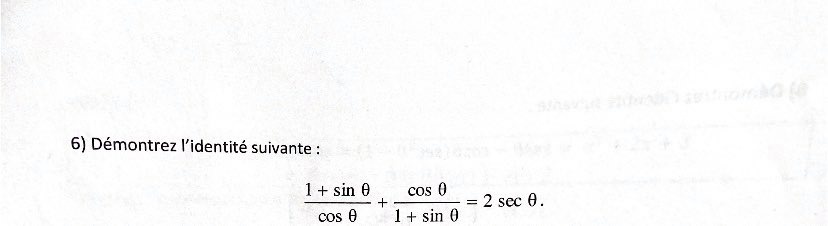






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut YakEfficace4227 😁
Merci pour ta question!
D'abord, voici les principales étapes que tu dois suivre pour faire des démonstrations d'identités trigonométriques.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tu peux aussi aller voir d'avantage de détails sur notre fiche.
Je te le dis tout de suite, la meilleure façon de devenir meilleur.e en démonstrations, c'est d'en pratiquer plusieurs toi-même pour développer ta logique!
Avec les démonstrations d'identités trigonométriques, il est aussi très important de connaître justement ces identités. En effet, cela va te permettre de mieux voir les manipulations, les transformations et les simplifications à faire durant ta démarche pour arriver à la réponse recherchée. Jusqu'à ce tu les apprenne, tu peux te créer un aide-mémoire!
Suite à ces informations, essayons maintenant de résoudre ton exemple ensemble.
Nous avons l'égalité suivante.
$$ \frac {1+sin\theta}{ cos\theta } + \frac { cos\theta }{1+sin\theta} = 2\,sec\theta \, $$
Choisissons de commencer par le côté gauche de l'égalité.
Mettons les deux termes de l'addition sur un dénominateur commun.
$$ \frac{(1+sin\theta)(1+sin\theta) +(cos\theta)(cos\theta ) }{(cos\theta)\cdot(1+sin\theta)}= 2\,sec\theta \, $$
Faisons les multiplications du numérateur.
$$ \frac{1+2sin\theta +sin^2\theta +cos^2\theta}{cos\theta (1 +sin\theta ) } = 2\,sec\theta \, $$
Sachant, selon les identités trigonométriques, que $$ sin^2\theta +cos^2\theta = 1, $$ remplaçons les valeurs dans la démarche par 1.
$$ \frac{1+2sin\theta +1}{cos\theta (1 +sin\theta ) } = 2\,sec\theta \, $$
Sachant que 1+1=2, additionnons.
$$ \frac{2+2sin\theta }{cos\theta (1 +sin\theta ) } = 2\,sec\theta \, $$
Mettons en évidence le facteur 2 du numérateur.
$$ \frac{2(1+sin\theta) }{cos\theta (1 +sin\theta ) } = 2\,sec\theta \, $$
Nous pouvons observer qu'il y a $$1+sin\theta $$ au numérateur ET au dénominateur. Simplifions le.
$$ \frac{2 }{cos\theta } = 2\,sec\theta \, $$
Sachant selon les identités trigonométriques que $$ \frac{1 }{cos\theta } = sec\theta \, ,$$ notre égalité devient la suivante.
$$ 2\,sec\theta = 2\,sec\theta \, $$
Et voilà, nous avons fini de le démontrer! J'espère que la réponse est assez élaborée à ton gout. Bonne étude! 😊
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!