Secondaire 5 • 3a
Bonjour, dans cette inéquation, je ne sais pas quoi faire pour trouver le x2. Est-ce que je me fie a mon cercle trigonométrique ou j'utilise la formule cos(pi/2-y)= sin y. Parce que les 2 façons donnent un x2 différent.
Merci!
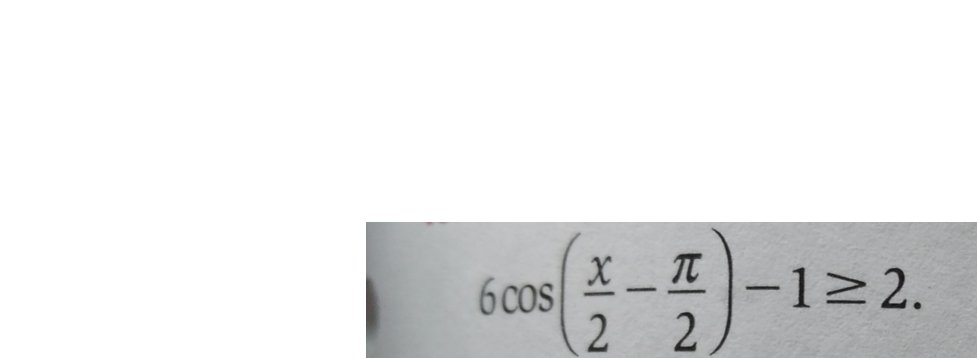






bonjour,
On peut aussi isoler le cosinus:
\[cos\left ( \frac{x}{2} -\frac{\pi}{2}\right )\geq \frac{1}{2}\]
\[ cos\left ( \frac{1}{2} \left (x-\pi \right )\right )\geq \frac{1}{2} \]
et résoudre mais c'est plus long.
Suggestion: tracer le graphique sur une période.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut Marion!
Pour ce numéro, tu dois te souvenir de l'identité suivante:
$$ \cos (y - \frac{\pi}{2}) = \sin(y) $$
Je te laisse déterminer la valeur de \(x\) en utilisant cette identité. :)
Voici une fiche AlloProf pour t'aider si jamais:
N'hésite pas à poser d'autres questions dans la zone d'entraide! :)
Charles
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!