Postsecondaire • 3a
Bonjour tout le monde! J'espère que vous allez bien.
Je ne sais pas comment répondre à cette question.
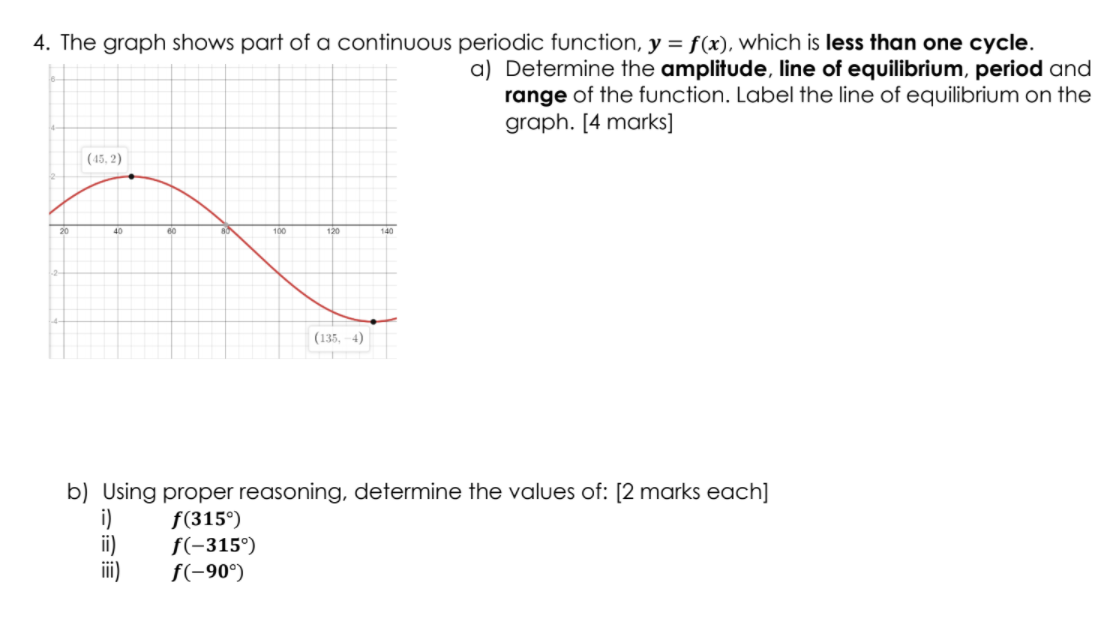
La traduction: Le graphique montre une partie d'une fonction périodique continue, y = f(x), qui est inférieure à un cycle.
a) Déterminez l'amplitude, la ligne d'équilibre, la période et l'étendue de la fonction. Indiquez la ligne d'équilibre sur le graphique.
b) En utilisant un raisonnement approprié, déterminez les valeurs de:
Merci!!






bonjour,
Écris tes réponses pour qu'on vérifie sinon précise ce que tu ne comprends pas dans les questions.
Il te suffit de cliquer sur les trois points en haut à droite de ta question pour l'éditer.
Note:
Pour répondre à b) on peut se servir du graphique et de la période.
i) f(315°)=f(315°-180°)=f(...°)=...
ii) f(-315°)=f(-315°-2*180°)=f(...°)=...
iii)f(-90°)=f(-90°+180°)=f(...°)=...
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut,
pour répondre à la question b), on devrait trouver la règle. Pour trouver la règle, on sera essentiellement obligé de répondre à a).
\[f(x) = a\sin\left(b(x-h)\right) + k\]
On voit que le maximum est \(2\) et le minimum est \(-4\). L'amplitude est \[|a| = \frac{2 - (-4)}{2} = \frac{6}{2} = 3\]
La line of equilibrium est \(y=k\). On trouve \[k = \frac{2 + (-4)}{2} =\frac{-2}{2} = -1\]
D'autre part, on voit que le maximum est à 45° et le minimum qui suit est à 135°. Puisque \(135^{\circ}-45^{\circ} = 90^{\circ}\) et qu'entre un maximum et un minimum il y a une demi-période, la période complète est donc \(90^{\circ} \times 2= 180^{\circ}\). La valeur de \(|b|\) est \[|b| = \frac{360^{\circ}}{180^{\circ}} = 2\]
Enfin, si on prend \(a\) et \(b\) positifs, on constate que le maximum arrive bien au premier quart de période (car \(180^{\circ} \div 4 = 45^{\circ}\)). Elle n'a pas subi de déphasage, donc \(h=0\).
\[f(x) = 3\sin\left(2x\right) - 1\]
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voilà ! À toi de jouer !
PS. Habituellement, lors de l'étude des fonctions trigonométriques, on utilise les radians. Ici, j'ai utilisé le sinus en degrés.
Aussi, si tu n'as pas vu tous les détails de la fonction sinus mais seulement les fonctions périodiques en général, (je vois que c'est écrit using proper reasoning), réécris-nous !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!