Bonjour,
Pouvez-vous me dire si ma démarche est adéquate svp?
Voici un trinôme:
Après l'avoir réécrit dans son bon ordre d'écriture (selon les conventions en algèbre), cela me donne: 4p^2 - 29p + 25
Puis j'utilise la méthode Somme et Produit (pour transformer le nouveau trinôme en polynôme à 4 termes), ce qui me donne:
4p^2 - 29p + 25
4p^2 - 25p - 4p + 25
Enfin, je fais la double mise en évidence:
4p^2 - 29p + 25
4p^2 - 25p - 4p + 25
p(4p - 25) - 1(4p - 25)
(4p - 25) (p - 1) <<< Rép. finale!
Cependant, lorsque je compare ma réponse finale avec mon amie, nous n'avons pas le même résultat. Elle a plutôt obtenu (25 + 4p) (1-p), car elle n'a pas réécrit le polynôme de départ dans le bon ordre selon les conventions d'écriture en algèbre.
Alors je me demande laquelle de nous deux a la bonne réponse???
Merci d'avance :)
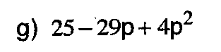






Je crois que tu as la bonne réponse! Il faut toujours réécrire dans la bonne écriture avant de faire notre factorisation :)
Ton amie a obtenu (25 + 4p) (1-p).
Si on effectue la multiplication, on a
(25 + 4p) (1-p)
= 25-25p+4p-4p²
= 25-21p-4p²
et ce n'est pas égal au trinôme initial.
------
Par contre,
25-29p+4p²
= 25-25p-4p+4p²
= 25(1-p)-4p(1-p)
= (1-p)(25-4p)
et ce pourrait être accepté car
(1-p)(25-4p)
= (-p+1)(-4p+25)
= -1(p-1)×-1(4p-25)
= +1(p-1)(4p-25)
= (p-1)(4p-25)
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut leylah!
Merci pour ta question et d'avoir ajouté ta démarche à ta question!:)
Il est effectivement nécessaire de réécrire le polynôme selon sa forme générale \( ax^2 + bx + c\). Ici nous avons donc \( a = 4\), \( b = -29 \) et \( c = 25 \).
J'ai la même démarche que toi pour la méthode produit/somme: Le produit doit donné \( a \times c\ = 25 \times 4\) et la somme \( b = -29 \).
Il est donc possible qu'une erreur se soit glissée si le polynôme n'est pas sous sa forme \( ax^2 + bx + c\). J'obtiens \((p-1)(4p-25)\) comme toi. :)
Bonne journée! :)
Charles
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!