Secondaire 5 • 4a
Bonjour, est-ce que c'est possible que mon prof s'est trompé. Il faut écrire a règle du graphique avec la fonction en rouge. C'Est possible que mon prof est oublié d'écrire (x+4), car sinon, je ne comprends pas comment mon prof est arrivé à cette règle avec ce graphique. Je ne comprends pas comment le h peut être à zéro, le point de départ est (-4, 0)....
Vous avez oublié de répondre à ma question :)
ESt-ce que a règle en rouge reprenste le graphique, ou c'Est une erreur?






Bonjour,
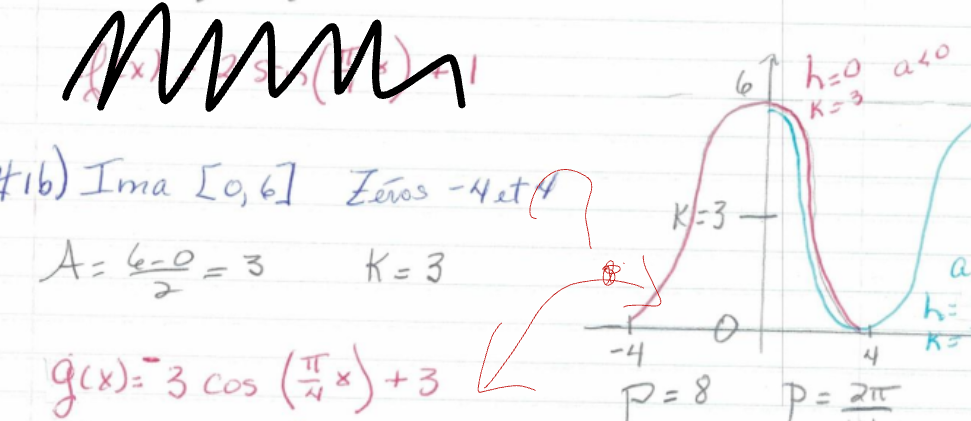
juste pour faire du pouce sur la réponse précédente... Plusieurs fonctions trigonométriques peuvent être représentées par un même graphique. Ainsi,
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
est le graphique de \[g_1(x) = 3\cos\left(\frac{\pi}{4}x\right) + 3\]
et de \[g_2(x) = -3\cos\left(\frac{\pi}{4}(x + 4) \right) + 3\]
Donc soit on met le moins devant le 3 et le \(x+4\), soit on ne met pas de moins devant le 3.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut Nath777,
Merci pour ta question!
Si tu traces le graphique de la fonction g(x)=-3cos(π/4x)+3, tu obtiens ce graphique :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Comme tu peux le voir, lorsque x = -4 y ne donne pas 0, il est au maximum. Pour l'avoir au minimum, tu peux changer le signe de a et tu obtiens ce graphique :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce graphique correspond à celui en rouge, mais l'équation n'est pas g(x), le signe de a a été changé.
Il y a donc une coquille entre le graphique et la fonction.
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!😉
Anthony B.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!