Secondaire 5 • 1a
Bonjour, ça fait déjà deux semaines que j'essaie de trouver la règle de la fonction en rouge et je n'arrive encore pas! Je n'en peux plus, pouvez vous me donner la réponse avec les explications? Merci beaucoup!






↓
Pour la courbe en bleu, il faut utiliser une fonction exponentielle de la forme
\[f(x)=a(0.7878)^x+k\ .\]
À l aide des 2 points, on écrit 2 équations qui permettent de déterminer les paramètres a et k.
Voilà!
P.S. La règle ne pouvait pas être de la forme \[f(x)=a(c)^x\] car cette forme ne coupe pas l axe des x, peu importe la valeur de c.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Allo!
Merci de nous faire confiance pour tes questions…
… et j’espère que ton attente de 2 semaines sera récompensée par mes explications.
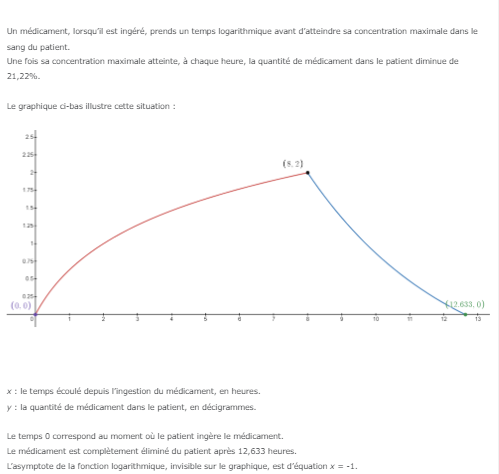
Donc la fonction « rouge » est une fonction logarithmique, passant par les points (0 , 0) et (8 , 2). Son asymptote est la droite verticale d’équation x = -1.
Dès maintenant, nous pouvons tirer la conclusion que le paramètre h = -1.
Le modèle canonique de la fonction log est le suivant :
F(x) = a logc b (x – h) + k
Cependant, à cause des lois des log et des exposants, il est toujours possible de simplifier ce modèle comme suit :
F(x) = logc b (x – h)
Comme nous savons que h = -1, il nous reste 2 paramètres à déterminer. Donc nous avons 2 inconnus. Et à CHAQUE fois qu’il y a 2 inconnus…. Il faut déterminer 2 ÉQUATIONS pour les trouver (système d’équations). C’est pour cette raison qu’ils nous ont donné 2 points dans la question.
Donc en remplaçant x et f(x) par les coordonnés des points déjà fournis, nous pouvons établir les 2 équations suivantes :
(8 , 2)……. 2 = logc b (8 +1) = logc 9b
(0 , 0)……. 0 = logc b (0 + 1) = logc b
Nottons ici qu’il faut écrire « +1 », puisque h = -1. Donc « x – h » devient « x – (-1) », donc x + 1
Nos 2 équations, une fois converties en forme EXPONENTIELLES deviendront ceci :
c² = 9b
c⁰ = b Mais comme c⁰ = 1, alors nous concluons que b = 1
En remplaçant « b » par « 1 », nous obtenons dans la première équation :
c² = 9(1) = 9
Donc c = 3
En conclusion, l’équation de la fonction log sera : f(x) = log₃ (x + 1)
Voila!
Surplus pour les personnes qui travaillent 2 semaines sur un problème :
L’équation bleue est : f(n) = 20,33 (0,7878)ⁿ - 1,017
J'utilise la lettre "n" seulement parce que je n'ai pas de "x" sur mon clavier en exposant....
Bonne chance pour la suite et n'hésite surtout pas à revenir nous voir si tu en a encore besoin!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!