Secondaire 4 • 1a
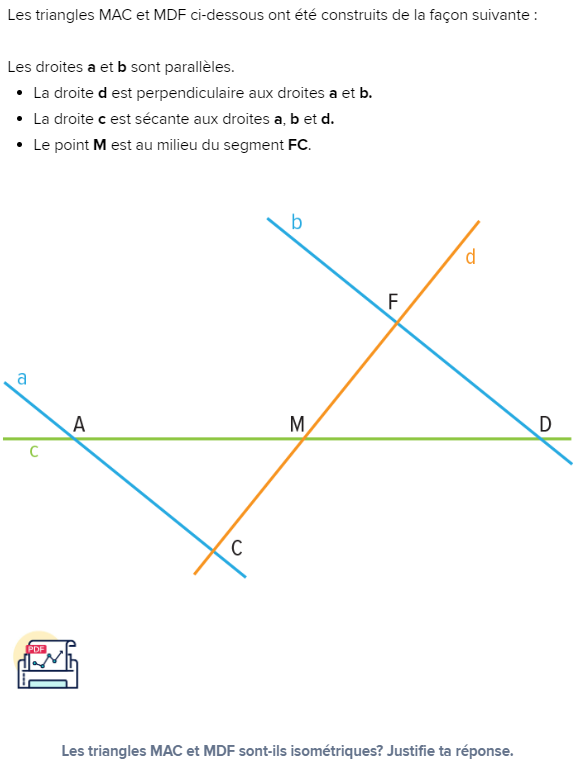
Salut! Ici, j'ai besoin de remplir un tableau affirmation/justification pour prouver que les deux triangles sont isométrique et ce par une conditions minimale d'isométrie. Mais lequel et comment le prouver? Je ne comprends pas bien la capsules explicative disponible sur le site! chaque justifications sont les même c'est a dire par hypothèse car l'informations est données sur le dessin mais que dois je faire ici? merci d'avance






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonsoir Zoe !
Merci de ta patience !
Comme tu le sais, il faut utiliser tes données et des propriétés et des théorèmes pour se rendre à la conclusion.
Je te recommande de commencer par la conclusion pour savoir de ou commencer : c'est quoi des triangles isométriques ? Quand tu te poses cette question, porte attention particulière à ta situation. Ainsi, tu réaliseras qu'il faut s'intéresser aux triangles rectangles.
Une propriété dit que deux triangles rectangles sont dits isométriques si un de leurs cotés est égale ainsi qu'un angle (autre que l’angle droit). Voilà la première étape. Maintenant, comment prouver cela ?
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-conditions-minimales-d-isometrie-des-triangle-m1265
En ce qui concerne le coté égale que tu recherches, tu sais que FM = MC car M est le milieu de FC. Comment le sais-tu ? Le point milieu est un point de partage qui sépare le segment initial en deux segments égaux, comme vu dans ce lien : https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-point-milieu-et-le-point-de-partage-d-un-segmen-m1313
En ce qui concerne l'angle égale que tu recherches, tu sais que les angles non adjacents formés par la rencontre de deux droites sécantes sont opposés par le sommet. Les angles opposés par le sommet sont isométriques.
As-tu des angles qui respectent cette caractéristique ?
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-relations-entre-les-angles-m1476
As-tu des sécantes ici ? Sache que des droites perpendiculaires sont des droites sécantes qui se coupent à angle droit puisque la pente de l'une est l'opposée de l'inverse de la pente de l'autre.
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-position-relative-de-deux-droites-m1318
Qu'en penses-tu ?
Salut!
Tu dois remplir un tableau de la formule suivante :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Dans la colonne affirmation, tu dois présenter les données que tu trouves, que ce soit pour les angles ou pour les droites. Dans la colonne justification, tu dois justifier ce résultat. Voici un exemple :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tu peux débuter ce tableau en inscrivant toutes les informations que tu connais, puis les justifier dans la section justification par "par hypothèse". Par exemple, tu peux écrire comme première affirmation a//b, puis dans justification "par hypothèse", ou encore FM=MC, car "M est le point milieu de FC par hypothèse".
Puis, c'est là que le vrai travail commence. Tu peux utiliser les différentes relations entre les angles pour déterminer les angles qui sont isométriques. Voici une fiche sur cette notion qui pourrait t'être utile : Les relations entre les angles | Secondaire | Alloprof
Tu devras justifier assez de conditions pour pouvoir conclure que les triangles sont isométriques par l'un des trois cas suivants :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Les conditions minimales d'isométrie des triangles | Secondaire | Alloprof
J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!