Secondaire 4 • 3a
Allo
Je ne comprend pas comment trouver l'angle de ce triangle provenant d'un exercice.
Utiliser cette équation: a/sin(A)=b/sin(B) mais il me manque un angle... Pouvez-vous m'aider svp? MERCI
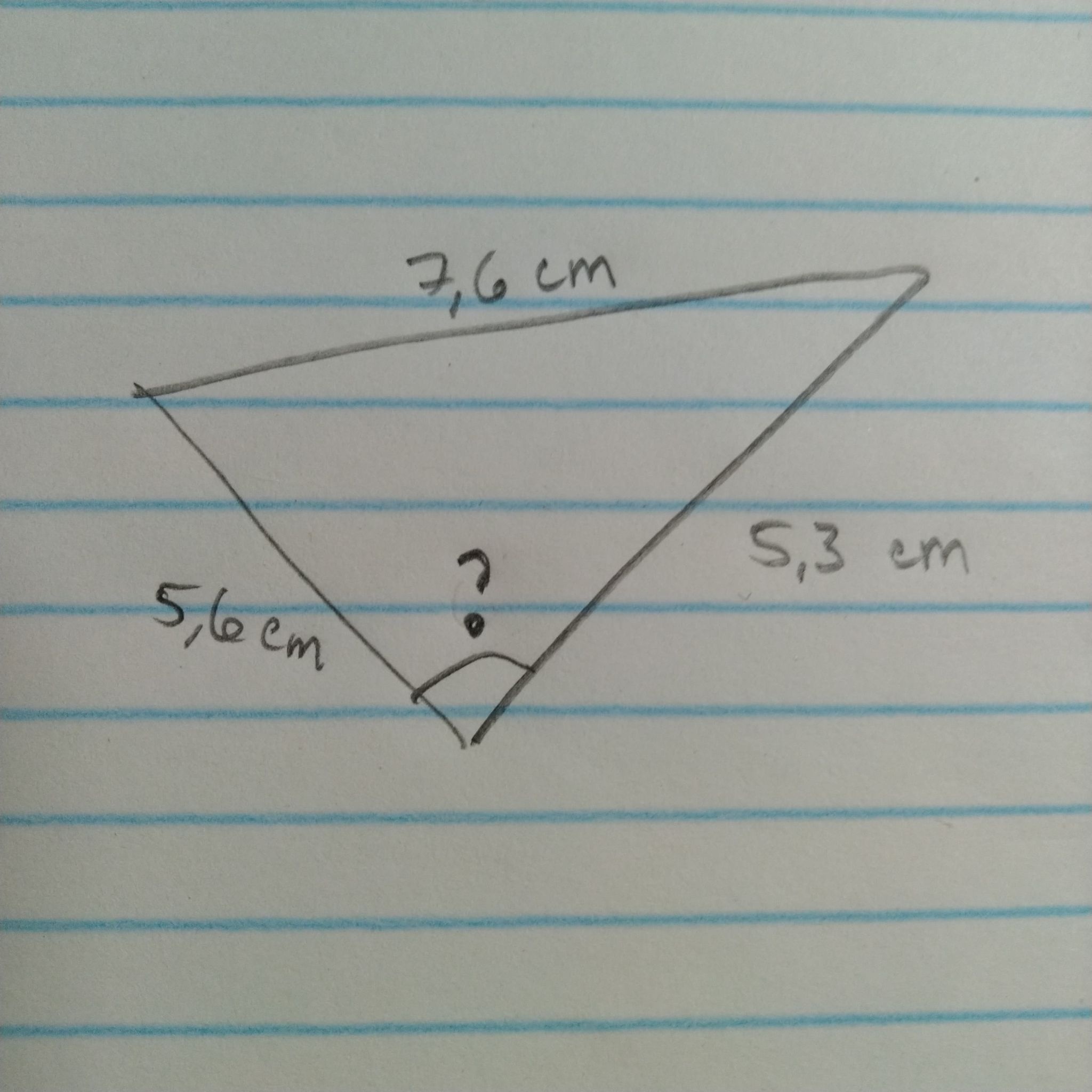






10,9 CM c'est bien sa au moins j'ai ésseillé quelque chose:)
Avec la loi des cosinus tu va être capable de trouver ton angle tu n'as pas la bonne formule regarde sur alloprof j’ai étudier ça l’autre jour et je sais qu'il l’explique très bien la formule tu dois déjà donner des lettres a tes sommets soient A,B etc. en majuscule puis directement face a c’est angles en minuscule tes mesures de tes côtés a,b,c ensuite tu prends la formule qui convient a au carré= b+c -2bc CosA le CosA c’est ton angle que tu cherches tu dois l'isoler mais je aais que ce n’est peut être pas très clair mais j’ai vu ton problème et je me suis dit que si je pouvais t’aider que ce serait tant mieux va voir sur la loi des cosinus sur alloprof ou internet tu va voir sa ressemble pas mal a et tu vas comprendre mieux
Faire une loi des cosinus pour trouver le cosinus et ensuite faire cos-1 sur la calculatrice
tu peux utilisier ton prof pour de l'aide.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonsoir loutrerusee28!
Effectivement, la loi des sinus ne peut être utilisée pour résoudre ton problème. La loi des cosinus par contre te permettrait de trouver l'angle manquant!
La formule générale pour la loi des cosinus est la suivante:
$$ a^2=b^2+c^2-2bc\cos A$$
Il faut donc isoler de l'équation l'angle en question, c'est-à-dire:
$$A = \arccos\left(\frac{b^2 + c^2 - a^2}{2bc}\right)$$
En utilisant la nomenclature suivante sur le triangle de ta question, il est possible de déterminer l'angle A qui est demandé dans ton problème.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Si tu as besoin de plus d'information concernant la loi des cosinus, je t'invite à visiter cette page de notre site web:
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-loi-des-cosinus-m1294
N'hésite pas si tu as d'autres questions!
Charles
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!