Secondaire 4 • 4a
Bonjour! J'ai commencé le problème suivant, mais je bloque à la résolution du système. Aidez-moi svp! Merci!
Edit : J'ai suivi votre conseil, mais malheureusement je bloque encore, qu'est-ce que je fait mal? (Le calcul modifié ci-dessous) Merci!
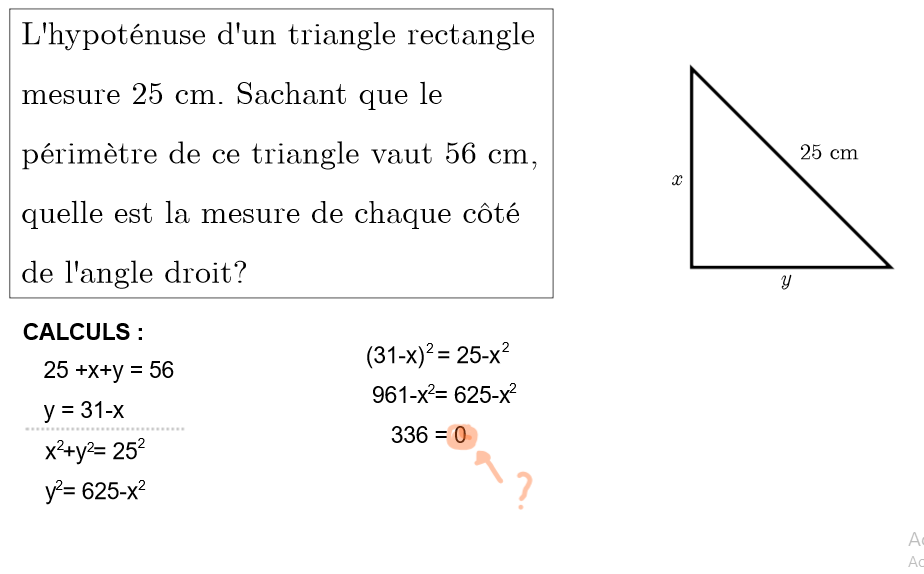






En faite, tu poses l'égalité donc
$$ (31-x)^2 = 625 - x^2 $$
Tu as écrit 25 dans ta 1re ligne à droite, mais tu devrais écrire 625 !
Par la suite, quand tu développes le (31 - x) au carré , l'exposant 2 ne se distribue pas de cette façon, mais bien de cette façon
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tu dois multiplier chaque terme avec les 2 autres termes de l'autre parenthèse, car le carré est appliqué à la parenthèse au complet.
Est-ce que c'est plus clair?
n'hésite pas s'il y a quoi d'autre
VC
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Salut,
Tu étais bien parti, cependant, tu ne peux pas faire la racine des 2 côtés et obtenir x+y = 25 . En effet, ceci vient fausser tes résultats, car ce si tu voudrais faire la racine des 2 côtés, tu aurais alors ;
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Dans une addition, la racine ne peut se séparer.
Pour procéder, il faut alors poser 2 équations et 2 inconnues !
La première équation est celle du périmètre comme tu l'as écrit
La deuxième équation est celle avec Pythagore
On obtient
$$ x^2 + y^2 = 625 $$
Tu peux donc isoler ton y au carré et poser l'équation
$$ y^2 = 625 - x^2 $$
Il ne te reste qu'à remplacer dans y, le développer au carré et résoudre !
J'espère t'avoir aidé à trouver ton erreur
Bonne continuation
VC
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!