Secondaire 4 • 3a
bonjour je suis en secondaire 4 TS il y a ce numéros 5 de a à L que je ne comprends pas stp je suis plus visuelle si je vois les solutions je peut comprendre et numéros 6 aussi a , b et c merci du fond du coeur .
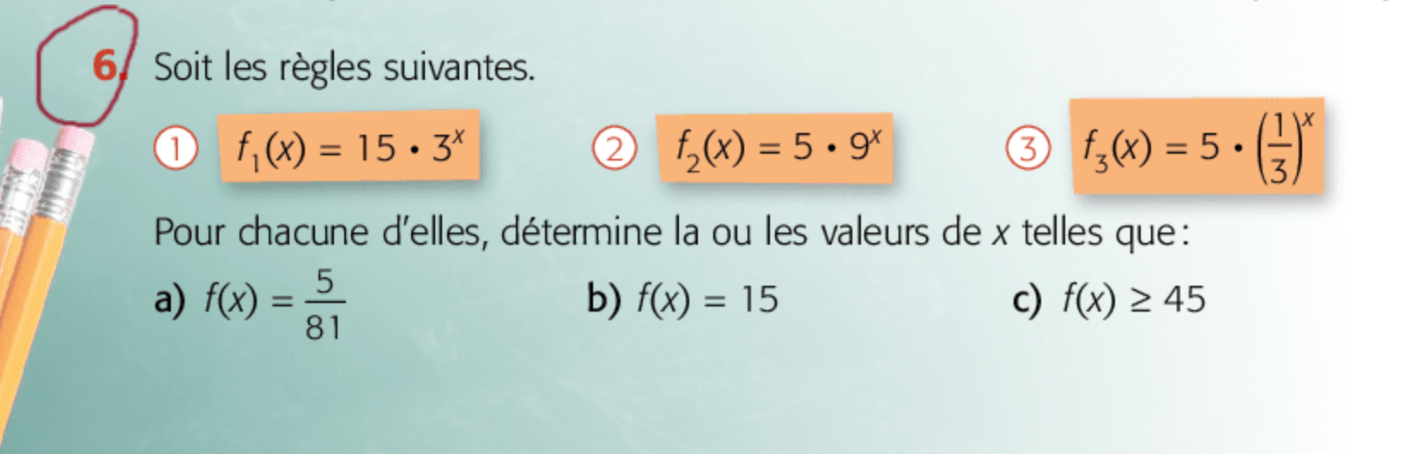







On peut faire sans logarithme.
On isole la puissance et quand les bases sont les mêmes, il faut que les exposants soient égaux pour avoir égalité.
Exemple: 5h
\(-4(3)^{3x}=-36\)
\((3)^{3x}=\frac{-36}{-4}\)
\((3)^{3x}=9\)
\((3)^{3x}=3^2\)
\(3x=2\)
\(x=2/3\)
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour 😊
Pour le numéro 5, tu dois résoudre les équations exponentielles dans une base identique.
Tu dois trouver la puissance donnée est égale à combien de fois il faut multiplier la base, qui correspond à l'exposant.
Pour faire ceci, utilise la formule suivante de la forme logarithmique:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour le numéro 6, tu dois trouver la valeur appropriée de x
Pour le faire, utilise les fonctions données et isole le x.
Tu vas donc remplacer chaque F(x) par la valeur numérique donnée. Tu vas diviser le coefficient des deux côtés de l'égalité pour la balancer. Ensuite, tu vas te trouver avec une base exposant x. Pour trouver le x, tu vas devoir utiliser ceci:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Petit exemple visuel:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Consulte cette page Alloprof au besoin pour plus de détails:
J'espère que mes explications t'ont aidé :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!