Allo, j'ai une petite question. Est-ce que vous pouvez me dire si j'ai le droit de faire ça au lieu d'écrire X1=-b- racine de delta... et X2=-b+ racine de delta...
(Voici l'équation utilisée: 2x^2 +3x-2=0)
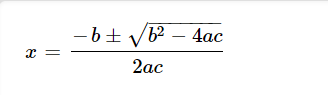
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Je fais la démarche et à la fin fin fin j'arrive à
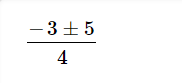
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
et qu'après ça j'écris:
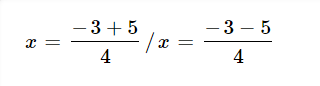
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
P.S.: La barre oblique (/) est utilisée pour dire ''Ou''
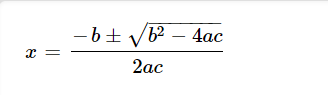
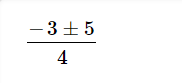
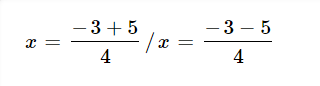






bonjour,
Le symbole «V» peut servir pour signifier «ou», pas la barre oblique qui est un symbole de division.
Bonjour,
D'abord, il y a une petite coquille dans la formule. Le tout est divisé par 2a, et non par 2ac, mais je crois que tu le sais selon tes calculs.
$$ x_{1,2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a} $$
Ensuite, tu as le droit en effet de calculer les deux résultats.
Non seulement tu peux différencier x1 de x2, mais tu peux aussi donner un résultat encore plus précis en allant au bout des calculs.
$$ x_1 = \frac{-3 + 5}{4}=\frac{2}{4}=\frac{1}{2} $$
$$ x_2 =\frac{-3 - 5}{4}=\frac{-8}{4}=-2 $$
Je te conseille de ne pas utiliser la barre oblique pour séparer tes réponses, mais plutôt une virgule. Pose aussi les indices 1 et 2 aux x puisque tu as deux valeurs différentes.
N'hésite pas si tu as d'autres questions!
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut !
La démarche est importante en effet. Toutefois, tu dois en effet écrire les deux réponses possibles. Ta réponse est bonne, mais il te faut réduire les expressions de chaque réponse et leur donner une appellation différente (exemple : \(x_1\) et \(x_2\)).
Si tu as d'autres questions, n'hésite pas !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!