Secondaire 4 • 3a
Trigonométrie:
Je comprend le principe de proportion, à quoi sa va servir.
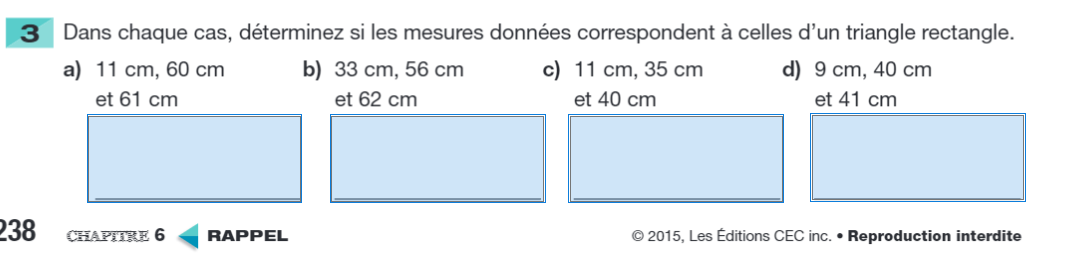
Dans mon cahier il est, écris 11cm, 60cm et 61 cm, tout en sachant que ad=bc, comment je définie lequel est a, lequel est b, lequel est c, lequel est d et laquelle des quatres letters est le x dans l'énoncé.
Point de mire p. 238 #3 a) si un prof veut voir de quoi je parle exactement.
Merci de répondre le plus rapidement possible.







Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut,
Pour ce numéro, tu n'as pas besoin d'utiliser des proportions, seulement du théorème de Pythagore.
Ainsi, afin de vérifier si les mesures données forment un triangle rectangle, il faut vérifier l'équation du théorème. Si elle marche, alors il s'agit bel et bien d'un triangle rectangle, sinon, ce ne l'est pas. La formule du théorème de Pythagore est :
$$ a² + b² = c² $$
où a et b sont les cathètes, et c l'hypoténuse.
Puisque le côté le plus grand d'un triangle rectangle est l'hypoténuse (côté opposé à l'angle droit), alors le côté mesurant 61 cm est nécessairement l'hypoténuse, et les deux autres mesures, 11 cm et 60 cm, sont les cathètes (côtés formant l'angle droit), si bien entendu il s'agit effectivement d'un triangle rectangle.
Posons donc l'équation :
$$ 11² + 60² = 61² $$
et vérifions si l'égalité est vraie :
$$ 11² + 60² = 61² $$
$$ 121 + 3600 = 3721 $$
$$ 3721 = 3721 $$
Nous avons ainsi pu confirmer que l'égalité est vraie, puisque nous avons obtenu le même résultat des deux côtés de l'équation. Par conséquent, le théorème de Pythagore est vérifié et nous pouvons donc affirmer que ces mesures forment bel et bien un triangle rectangle.
Pour en savoir plus sur le théorème de Pythagore, tu peux consulter la fiche suivante:
J'espère que cela répond à ta question et n'hésite pas si tu en as d'autres :)
Katia
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!