Secondaire 4 • 2a
Bonsoir! Désolé, mais je ne comprends toujours pas pourquoi la réponse est [800,99]. Je comprends que la partie entière soit 800 mais quel est le rôle du [8,3x] pour que la réponse finale soit [800.99] ? La partie entière de 8,3 est 8, non? J'ai un examen demain mais c'est la seule chose que je ne comprends pas.
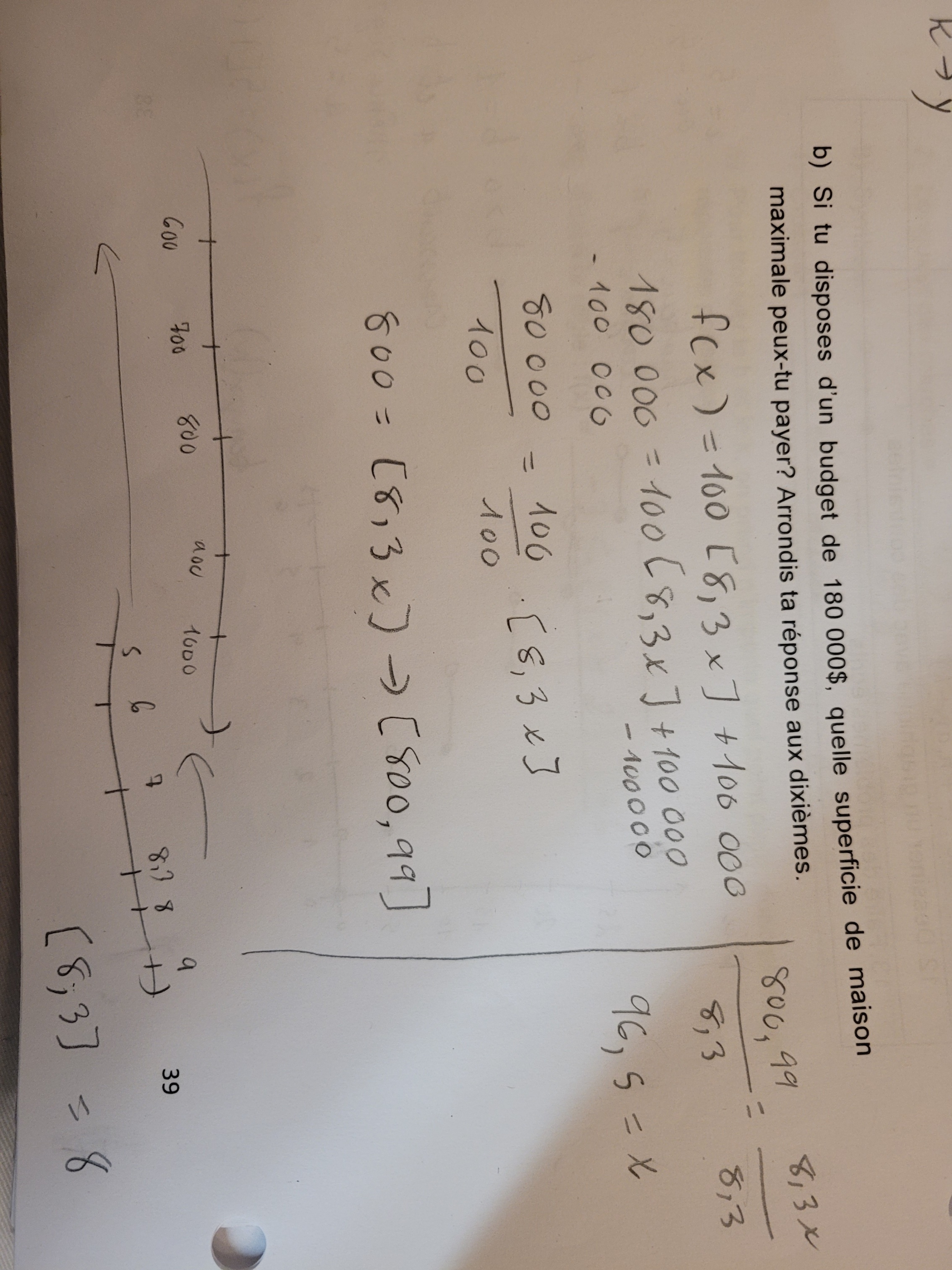






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Re salut!
Oui, la partie entière de
8,3est 8, mais ici, on a8,3x, et non 8!Puisqu'on cherche à résoudre l'équation, donc à isoler la variable x, il faut absolument éliminer la partie entière, puisqu'elle nous empêche de poursuivre la résolution. On a :
$$ 800 = [8,3 x] $$
Jusqu'ici tout va bien, n'est-ce pas? Cependant, là, on est bloqué. À cause de la partie entière, on ne peut pas simplement diviser les deux côtés de l'équation par 8,3.
Donc, on doit réfléchir. À cette étape, on doit se poser la question suivante : la partie entière de quels nombres donne 800?
La réponse est tout l'intervalle entre 800 et 800,9999...
Il faut alors remplacer le côté gauche de l'équation par les bornes de cet intervalle, ce qui nous permet d'éliminer la partie entière :
$$ 800 = 8,3 x $$
et
$$ 800,99 = 8,3 x$$
On aurait alors eu un intervalle de valeurs possibles pour x de 96,39 à 96,5.
En d'autres mots, notre superficie peut se situer dans cet intervalle-là.
Puisqu'on cherche la superficie maximale, on va donc prendre la borne supérieure, soit 96,5.
Ainsi, si ça peut t'aider, je te conseille de prendre en compte le fait qu'on cherche le minimum ou le maximum à la toute fin du problème, comme je l'ai fait, et non au milieu du calcul comme tu l'as fait, c'est moins mélangeant et plus facile à comprendre.
Est-ce que c'est plus clair pour toi? Réécris-nous si ce n'est pas le cas, je vais rester en ligne encore un moment :)
PS Ne dors pas trop tard, tu dois être en forme pour ton examen de demain ;)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!