Postsecondaire • 2a
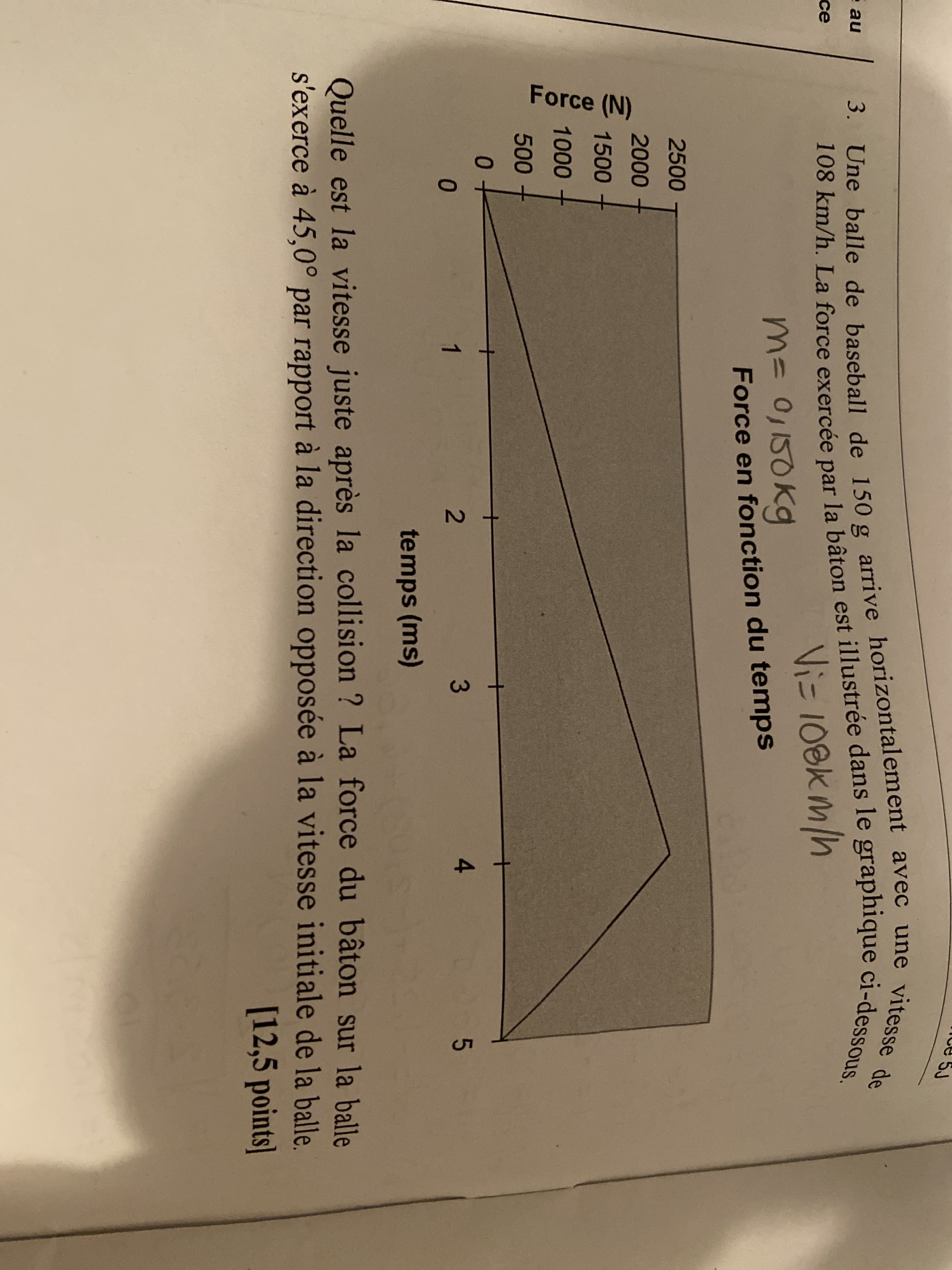
Bonjour, je n’arrive pas à trouver comment procéder pour ce numéro. Je sais que je dois faire l’intégrale de Fx dt=mVx, sauf que je ne comprend pas comment. J’ai attaché une photo ci-dessous. Merci!!






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Merci pour ta question!
D'abord, faisons un schéma du problème afin de mieux comprendre la situation :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Le problème ne mentionne pas de quelle type de collision il s'agit, mais il faut assumer, pour simplifier le problème, qu'il s'agit d'une collision élastique, c'est-à-dire, une collision dans laquelle la quantité nette d'énergie cinétique est conservée. Ceci nous permet d'établir que l'énergie cinétique initiale est égale à l'énergie cinétique finale du système :
$$ E_{k,i} = E_{k,f} $$
On peut encore plus développer ces équations puisque :
$$ E_k = \frac{1}{2}•m•v^2 $$
• Ek : énergie cinétique (n)
• m : masse (kg)
• v : vitesse (m/s)
Puisqu'il s'agit ici d'une collision élastique, l'équation sera donc la suivante :
$$ \frac{1}{2}•m_1•v_{i,1}^2 + \frac{1}{2}•m_2•v_{i,2}^2 = \frac{1}{2}•m_1•v_{f1}^2 + \frac{1}{2}•m_2•v_{f,2}^2 $$
Où les indices 1 et 2 représentent les deux objets (le bâton et la balle) et les indices i et f représentent les états initiaux et finaux de l'énergie.
À noter que nous aurions pu utiliser l'équation des collisions élastiques (que tu as probablement apprise)...
$$ m_1•v_{i,1} + m_2•v_{i,2} = m_1•v_{f1} + m_2•v_{f,2} $$
...mais que nous ne connaissons pas la masse et la vitesse du bâton, seulement son énergie, ainsi, il faut utiliser l'équation sous sa forme plus complète, ce qui nous permet de remplacer un des termes par la valeur d'énergie cinétique du bâton.
Bref, notons les valeurs que nous connaissons. Établissons que le bâton est l'objet 1 et que la balle est l'objet 2 :
$$ E_{i,1}= \frac{1}{2}•m_1•v_{i,1}^2 = \frac{1}{2}•0,150•(108\:km/h)^2 = \frac{1}{2}•0,150•(30\:m/s)^2 = 135\:N $$
$$ E_{i,2}= 2000\:N $$
Note : j'ai trouvé l'information ci-dessus dans le graphique. Le maximum de l'énergie du bâton correspond à son énergie initiale, car c'est à ce moment qu'il frappe la balle.
$$ E_{f,1} = \frac{1}{2}•m_1•v_{f,1}^2=\frac{1}{2}•0,150•v_{f,1}^2 $$
$$ E_{f,2} = 0\:N $$
Note : encore une fois, j'ai trouvé cette information dans le graphique; le bâton semble avoir transmis toute son énergie cinétique initiale à la balle.
Ainsi, il ne reste qu'à appliquer ces valeurs dans l'équation :
$$ \frac{1}{2}•m_1•v_{i,1}^2 + \frac{1}{2}•m_2•v_{i,2}^2 = \frac{1}{2}•m_1•v_{f1}^2 + \frac{1}{2}•m_2•v_{f,2}^2 $$
$$ 135\:N + 2000\:N = \frac{1}{2}•0,150•v_{f,1}^2 + 0\: N $$
Puis, tu dois isoler la valeur de v f,1.
Il se peut que ceci ne soit pas la bonne démarche au problème. En effet, ton enseignant.e. voulait peut-être que tu n'assumes pas qu'il s'agit d'une collision élastique, ou que tu considères l'orientation de la vitesse comme étant une valeur importante. Les cas échéants, tu peux reposer ta question en précisant qu'il ne s'agit pas de la bonne démarche.
Cette fiche du site d'Alloprof explique l'énergie cinétique :
N'hésite pas si tu as d'autres questions!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!