Zone d’entraide

CyclopeSigma5376

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Bonjour j'ai quelque difficulté pour ce problème. Je comprends que je dois trouver le maximum et le minimum de la fonction pour donner l'image. Cependant lorsque je remplace x et y dans mon équation par le points 5,2 et que j'essaie d'isoler le a, j'arrive a des réponses assez impossible. Je ne crois pas m'y prendre de la bonne façon. Merci d'avance.

AvocatTenace6777

bonjour Cyclope,

ton erreur était que

tu calculais cos(pi/3)×5=0,5×5

au lieu de cos(pi/3×5)=cos(5pi/3)=0,5.

FerUpsilon5520

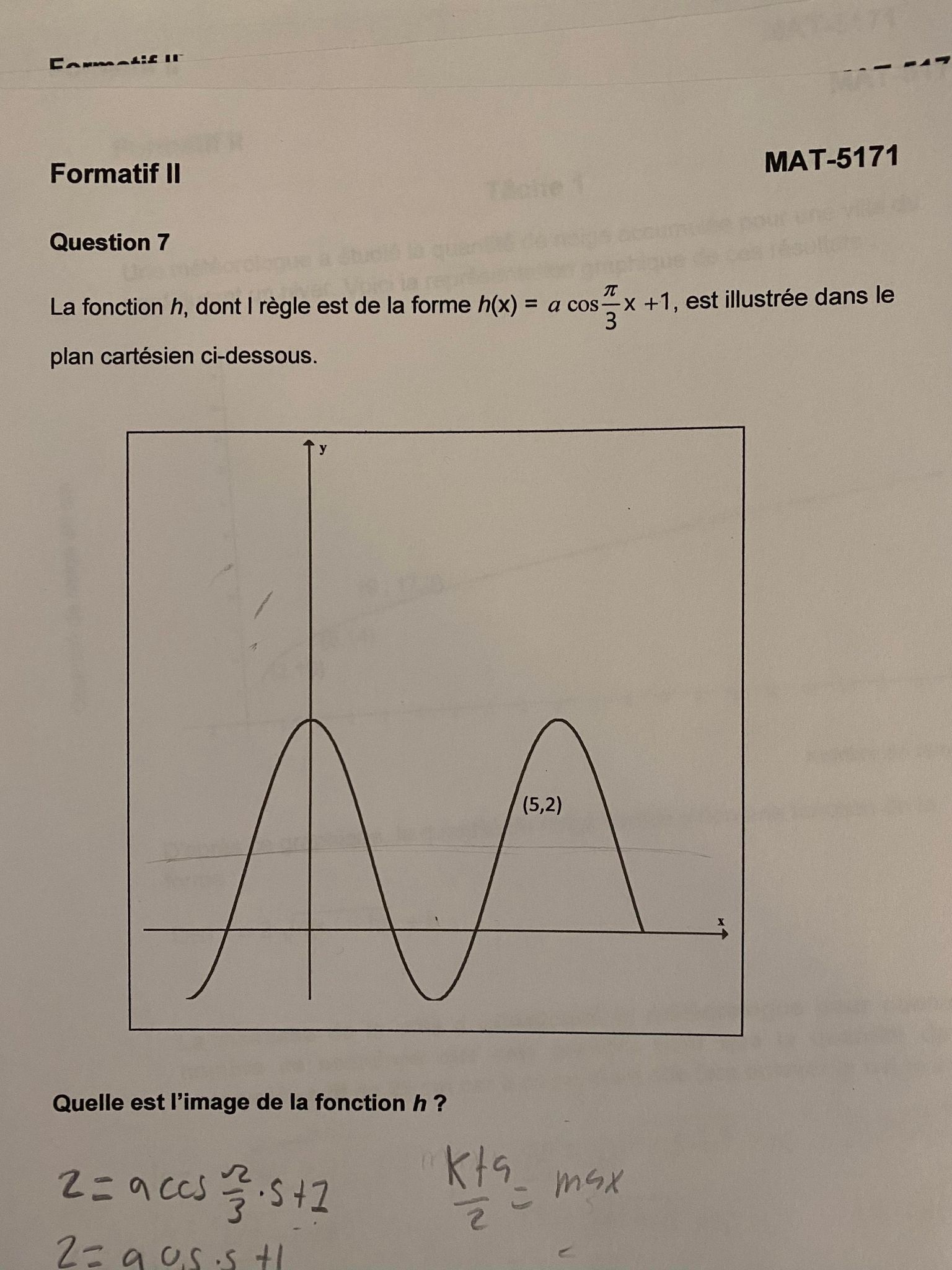
La fonction est h(x) = a cos (πx/3) + 1

Pour déterminer a on utilise le point (5,2) =>

2 = a cos (π5/3) + 1

or on sait que cos (5π/3) = 1/2 voir le cercle trigonométrique (https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-cercle-trigonometrique-m1389)

donc

2 = a . 1/2 + 1 ou 2 = a/2 + 1

1 = a/2 => a = 2 et h(x) = 2 cos (πx/3) + 1

or la fonction cosinus oscille entre -1 et +1 (à moins de restrictions sur son domaine - ce qui n'est pas le cas ici)

donc le maximum et le minimum de h(x) sont

2 . 1 + 1 = 3

et

2 . (-1) + 1 = -1