Secondaire 5 • 3a
Bonjour allo prof, je suis bloqué sur ce problème mathématique. Je comprends qu'il faut soustraire une équation à l'autre cependant, je n'arrive pas à réduire mes fonctions valeurs absolues. Merci d'avance de votre aide.
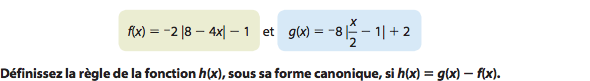






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour,
Dans ce problème, on souhaite simplifier :
h(x) = -8 | x/2 - 1 | + 2 + 2 | 8 - 4x | + 1
Maintenant, essaye de trouver une équivalence entre -8 | x/2 - 1 | et 2 | 8 - 4x | pour continuer.
Indice : sort un 4 de 2 | 8 - 4x | on obtient 2*4 | 2-x |. Par la suite, essaye de transformer la deuxième partie ( -8 | x/2 - 1 | ) de façon ce que les deux valeurs absolues soit équivalentes.
Il ne te restera plus qu'à regrouper les termes semblables et simplifier.
Bonne journée
Un indice:
| x - 2 | = | -(2-x) | = | 2 - x|
avec quelques simplifications tu verras que h(x) est assez facile à trouver.
bonjour,
on transforme l intérieur des valeurs absolues en mettant en évidence le coefficient de x.
on applique la propriété "la valeur absolue d un produit égale le produit des valeurs absolues".
Exemple:
\[ \left | 6-2x \right | \]\[ =\left | -2(x-3) \right |\]\[=\left | -2 \right |\left | x-3 \right |\]\[=2\left | x-3 \right | \]
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!