Secondaire 5 • 3a
Bonjour,
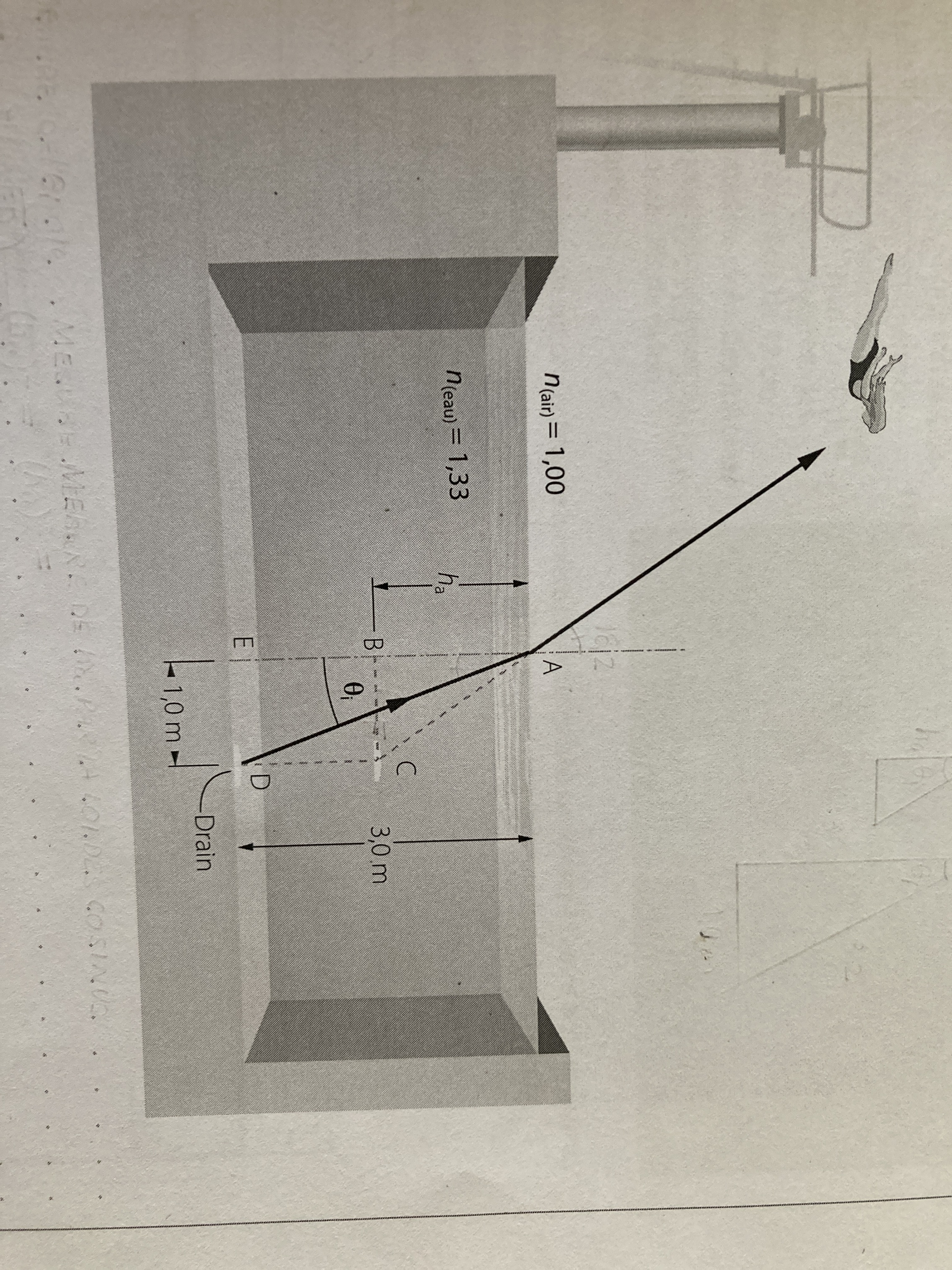
Je ne parviens pas à résoudre ce problème : Une plongeuse voit le fond de la piscine plus près qu’il ne l’est en réalité. À l’aide des données du dessin (photo jointe), calculer la profondeur apparente (ha) du drain, la vraie étant de 3,0 m, sachant que l’image du drain se trouve directement au-dessus de lui. Dessin pas à l’échelle. Il faut utiliser les propriétés des triangles rectangles.
Merci!






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut !
Il s'agit d'un exercice en plusieurs étapes. Dans un premier temps, il te faut calculer l'angle \(\theta _i\). Pour ce faire, tu dois utiliser la trigonométrie avec les valeurs de 1,0m et 3,0m.
Par la suite, tu dois calculer l'angle à l'extérieur de l'eau à l'aide de Snell-Descartes :
Finalement, cet angle (angle opposé) te permettra de calculer la hauteur avec la valeur de 1,0m.
Je te laisse essayer par toi-même et si tu as d'autres questions, n'hésite pas !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!