Bonjour,
je suis complètement bloqué
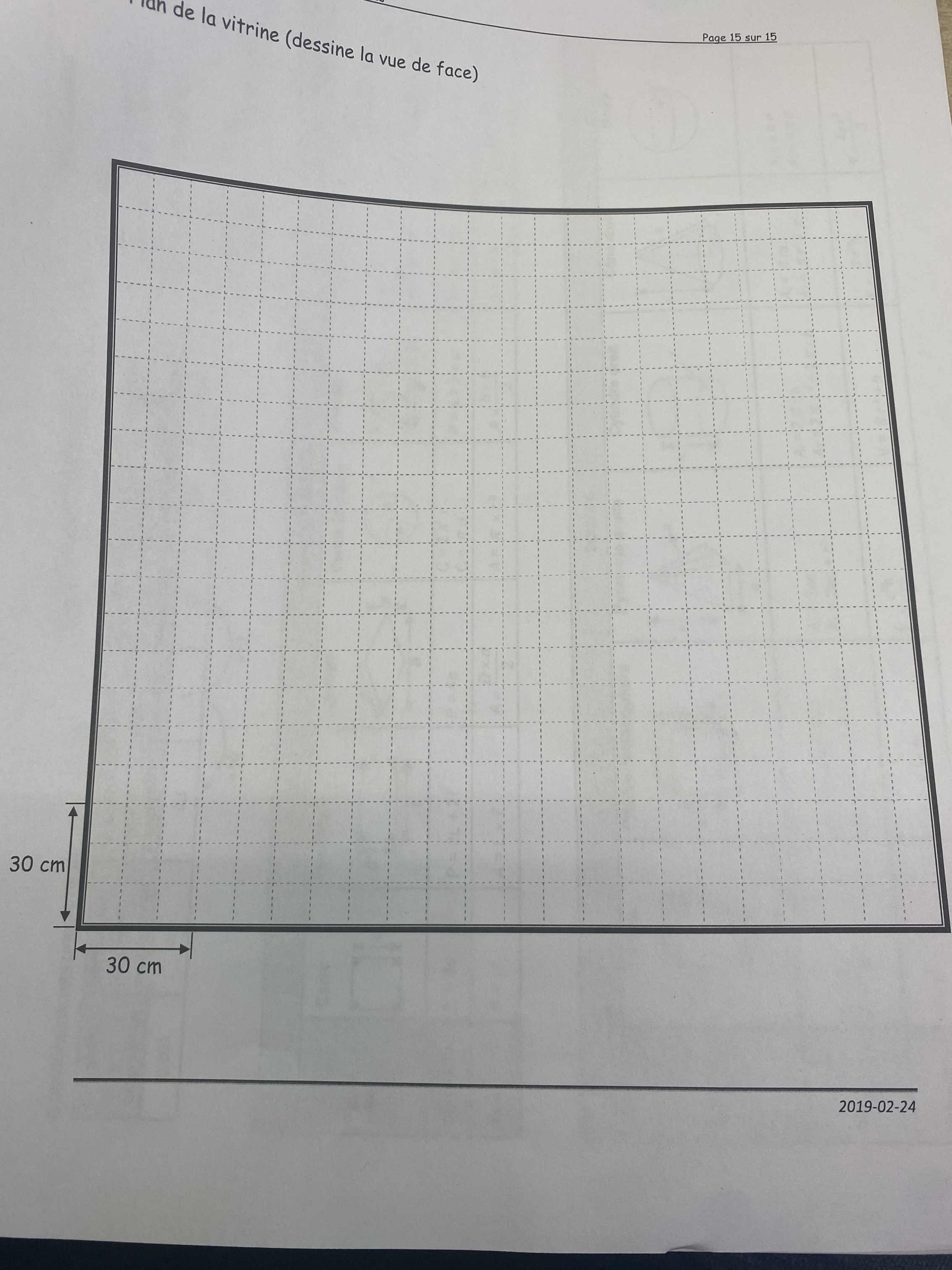
comment procéder pour faire le plan à l’échelle?
merci

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Salut :)
On a dessiné la vitrine. Chaque carreau vaut 10 cm x 10 cm.
On dit qu'il doit y avoir au moins deux étagères et que les solides décoratifs qui sont en bas ne sont pas sur les étagères, donc on peut dessiner les étagères en partant d'en haut.
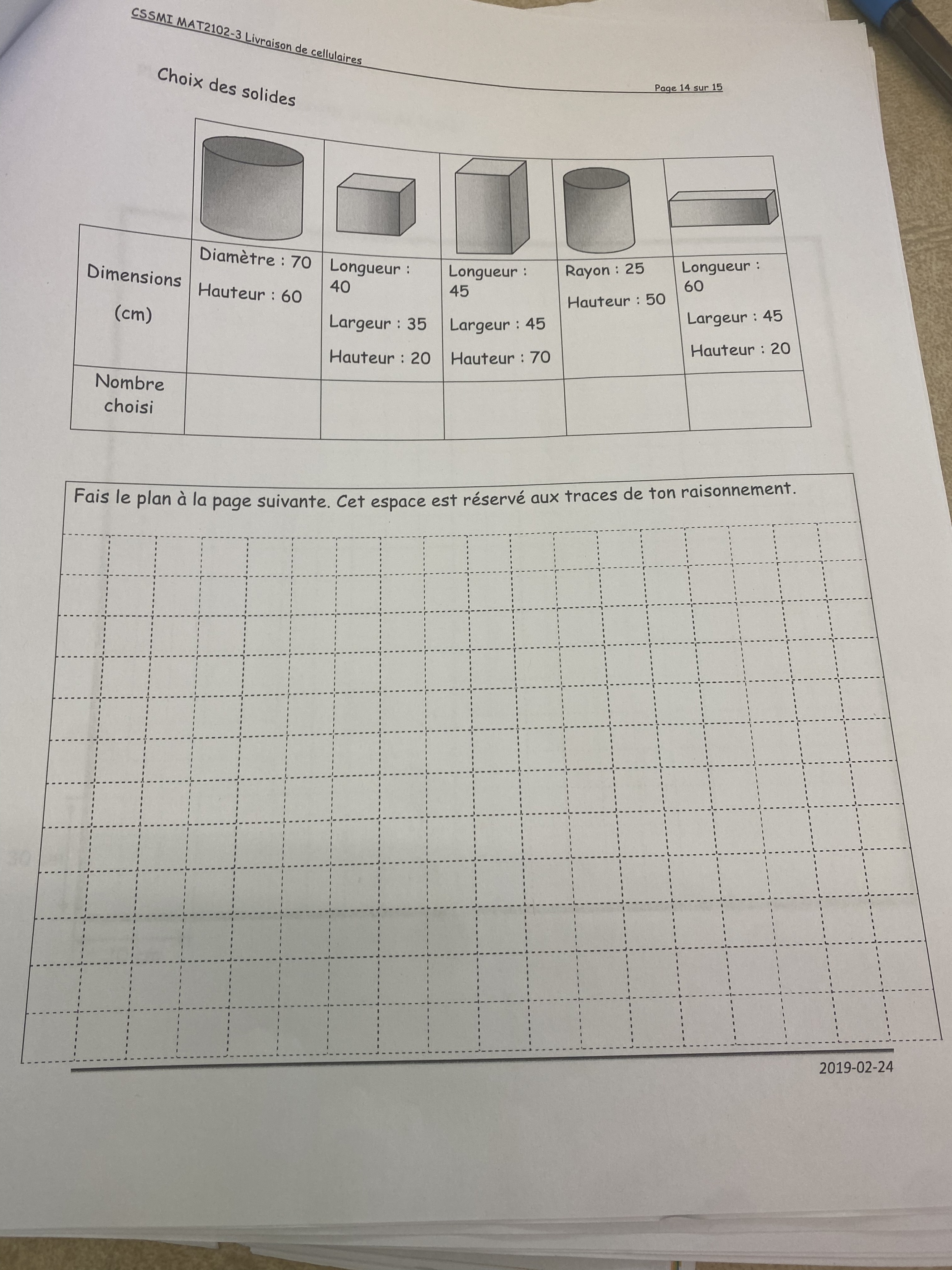
Pour les solides, ce avec quoi je commencerais, on dit qu'ils occupent entre 50% et 60% du bas de la vitrine. Donc, entre 50% et 60% de la partie en vert. (Quand on dit "entre", on n'inclut pas 50% ni 60%.)
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
L'aire de cette partie en vert est
profondeur * largeur = 2,2m*60cm = 220m*60cm = 13 200m²
Puis, l'aire que doivent occuper les solides sera d'entre (50% * 13200m²=) 6600m² et (60% * 13200m²=) 7920 m².
Voici les formules pour trouver les aires de la base des différents solides :
Après avoir placé au moins deux solides, place au moins deux étagères.
Et voilà, tu as résolu ce problème! :)
En espérant t'avoir aidé(e)
Chaque petit carreau du plan mesure 10cm par 10 cm
Il y en a 22 horizontalement et 20 verticalement.
Ça adonne bien tu ne trouves pas?
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!