Secondaire 4 • 2a
Salut, a quoi sert un point test (0,0) c’est en géométrie analytique je pense, mais je ne sais pas comment l’utilisé et comment on sait qu’elle signemettre dans une inéquation je suis perdu 😅dernière question quand est ce qu’on sait qu’il fait switcher notre signe de coter ? Pendant une multiplication ou une division ?
Merci d’avance !!






Sur "quand switcher notre signe de côté"
Pour une quelconque égalité (ou inégalité) disons
y - 4 = 3x + 17
je veux par exemple isoler le y. Alors pour "switcher le -4" de l'autre côté, j'additionne +4 des deux côtés de l'équation, ce qui équivaut à passer le -4 de l'autre côté en lui changeant de signe ( de - à + ).
MAIS CE QUI EST IMPORTANT C'EST SURTOUT QUE TU MAINTIENS L'EGALITE - TU N'AS RIEN CHANGE CAR TU AS ADDITIONNE LA MÊME QUANTITE DES DEUX COTES DE L'EQUATION.
(cette méthode s'applique à toute autre opération sur une égalité)
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
La géométrie analytique c'est génial (Merci M. Descartes)
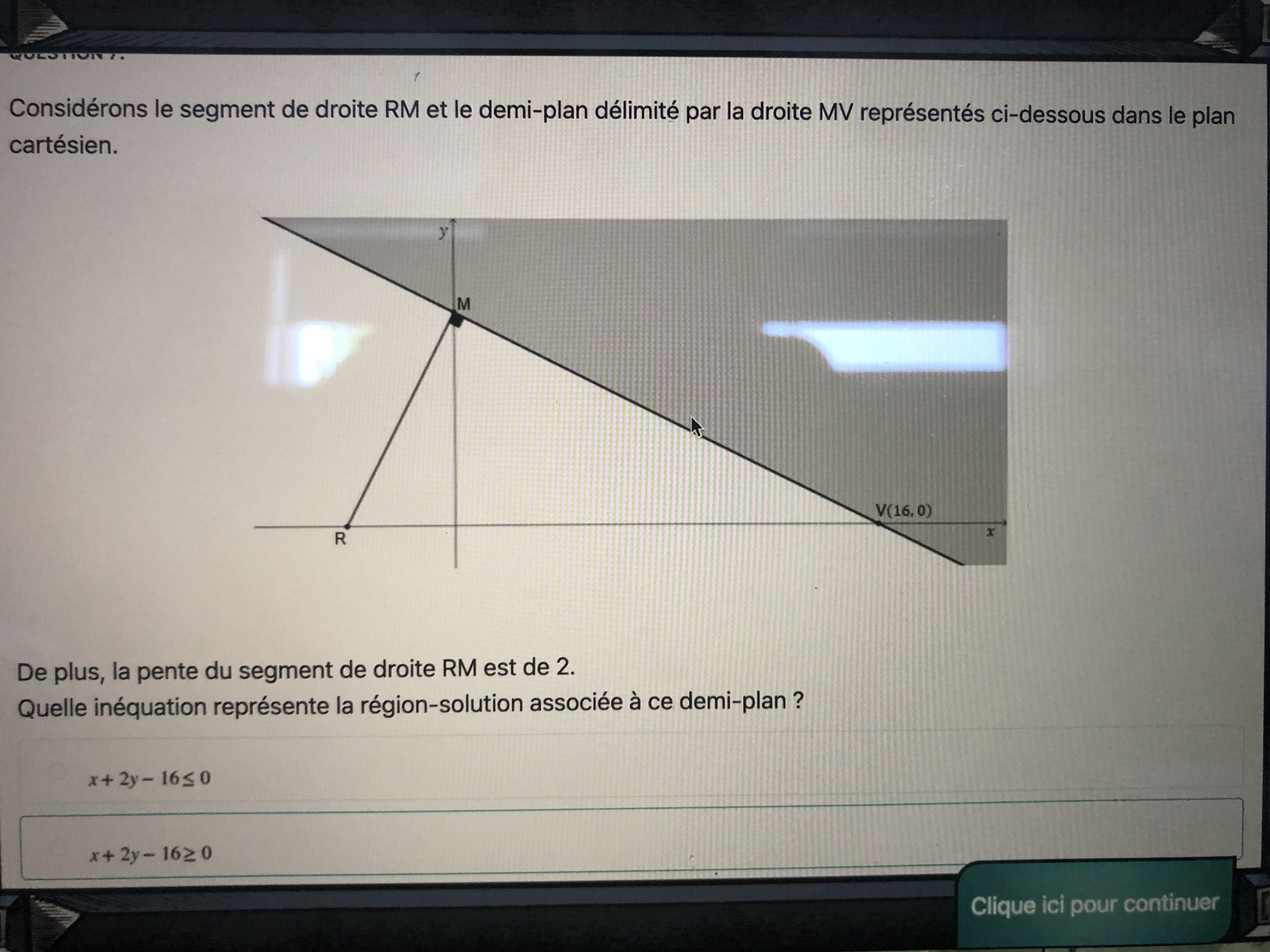
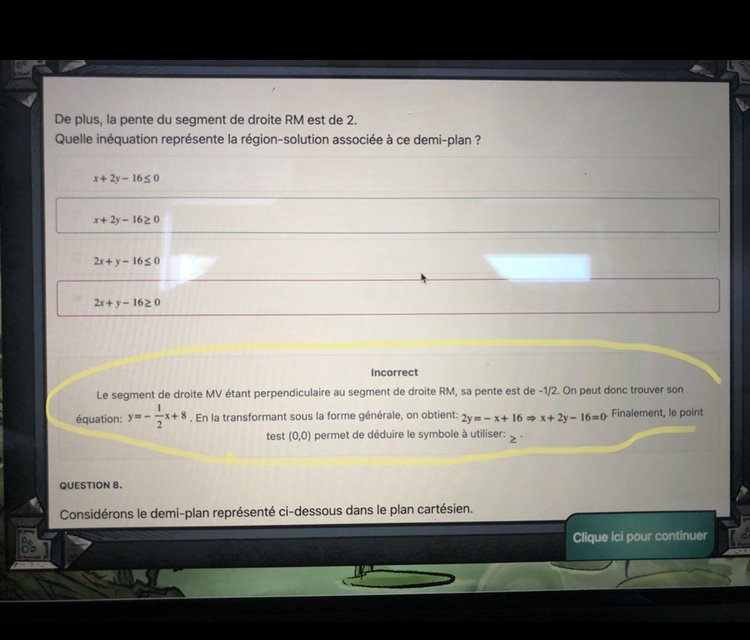
Comme la pente de RM est de 2 et est perpendiculaire à la droite dont on veut trouver l'équation, on sait que sa pente est de -1/2
donc on a y = - x/2 + b
cette droite passe aussi par le point (16, 0)
=> 0 = - 16/2 + b => b= 8
donc y = - x/2 + 8
ou encore x + 2y - 16 = 0
Pour savoir si le demi-plan est x + 2y - 16 ≥ 0
ou x + 2y - 16 ≤ 0
tu remplaces (x, y) par (0, 0) qui comme tu le sais n'est pas dans le demi-plan
et 0 + 2.0 - 16 = -16 ≤ 0 donc c'est l'autre demi-plan qu'il faut choisir!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!