Secondaire 5 • 2a
Salut!
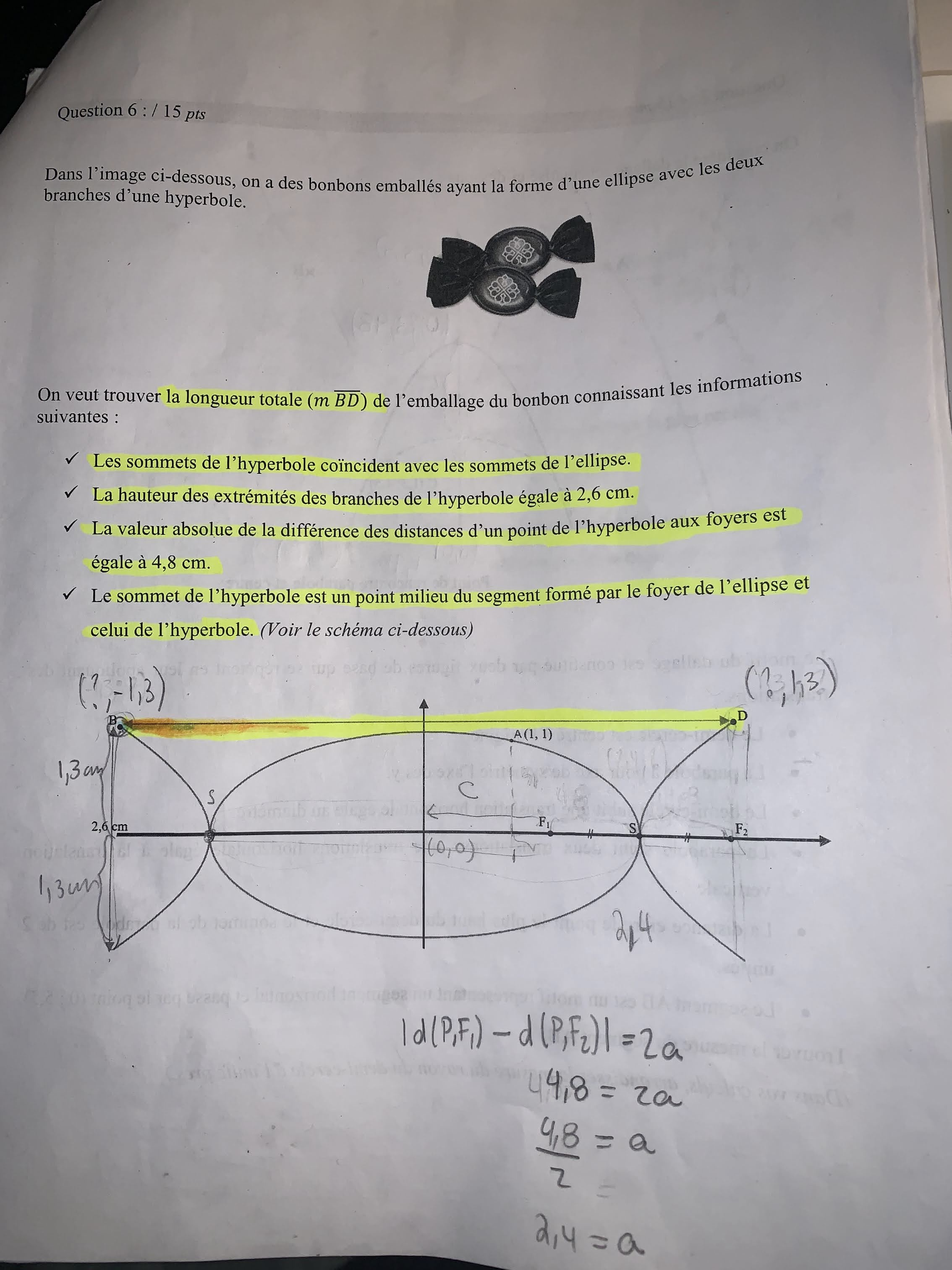
J'essaie de trouver la valeur de c pour l'ellipse mais je n'y arrive pas. J'ai trouvé la valeur de a, qui est aussi le sommet del'hyperbole et qui est le point milieu entre la distance des deux foyers dans l'image.







bonjour,
Un autre problème qui démontre qu il ne faut pas se fier à la figure pour estimer les coordonnées d un point.
F1 (2.133, 0) !
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Salut ! :D
Voici deux fiches :
Ellipse
Hyperbole
Avant de continuer, remarquons que tu as fais deux petites erreurs :
Le y du point B est 1,3 et non -1,3.
Le point A n'est pas placé sur l'axe vertical de l'ellipse, donc, le y du point A n'est pas b. Puis, avec l'ellipse, on utilise Pythagore. Ne te mélange pas non plus avec le foyer, "h" et l'équation de la directrice de la parabole.
Le sommet de l'ellipse est le même que celui de l'hyperbole qui est (2,4; 0). On a un point et le "a" de l'ellipse. On est en mesure de calculer la valeur de b.
Quand on aura "a" et "b", on pourra calculer "c" de l'ellipse, pour déterminer "c" de l'hyperbole (les deux "c" sont à égale distance du sommet).
Puisque "±c" correspond aux "x" de B et D, on est capable de trouver la valeur de mBD.
Bon exercice ! :)
Modification : ma démarche
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!