Secondaire 2 • 3a
Bonjour,
Je ne comprends pas pourquoi il y a un résultat dans l'ensemble de l'événement B et 6 dans l'ensemble des autres événements dans ce problème sur les probabilités avec un diagramme de Venn :
Une boîte contient 15 boules numérotées de 1 à 15. On choisit une boule au hasard et on observe le nombre. Voici deux événements possibles
A : « obtenir un nombre impair »
B : « obtenir un multiple de 5 »
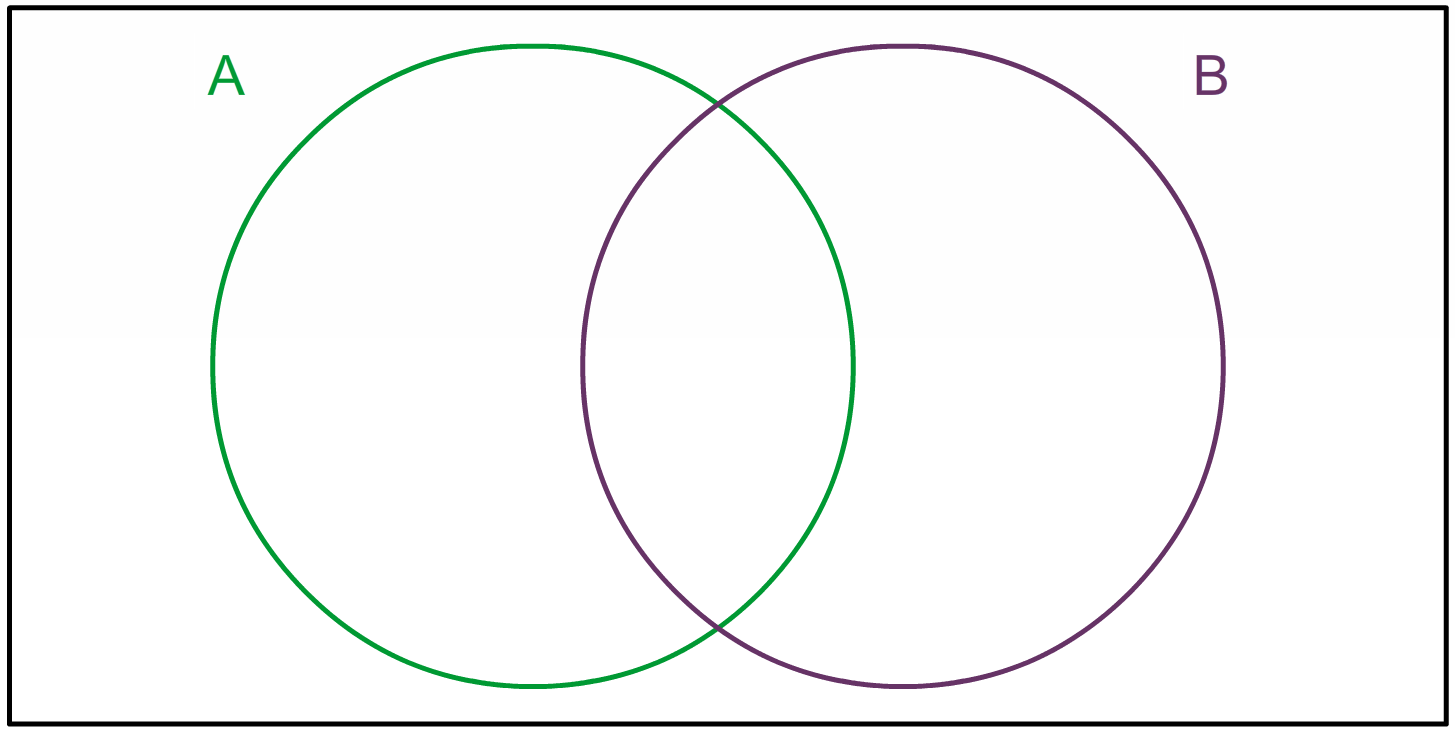
Complète ce diagramme de Venn en indiquant le nombre de résultats.
( Il y a 1 dans l'ensemble B, 6 dans aucun des deux ensembles, 2 dans l'intersection des deux ensembles et 6 dans l'ensemble A)
Merci






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut Maheva,
Merci pour ta question!😊
Pour répondre à ta question, je vais t'aider à faire le dénombrement de ta situation.
Pour ce qui est de l'évènement A, tu dois ressortir les boules qui ont un nombre impair parmi les 15, il y en a 7. Par contre, parmi les 7 tu ne sais pas combien sont aussi dans la catégorie B, qui est d'obtenir un multiple de 5. Dans cette catégorie, il y a 3 boules, 5, 10 et 15.
Avant de te jeter dans les boules qui se retrouvent dans les deux évènements, regardons celles qui n'en font pas partie. Si tu retires toutes les boules impaires et les multiples de 5, il te reste seulement 6 boules, qui sont 2,4,6,8,12 et 14. Pour ta question des 6 boules dans d'autres évènements, voici ta réponse.
Maintenant pour les boules dans l'intersection et les groupes A et B. Parmi les boules impaires tu as deux multiples de 5, soit 5 et 15. Ainsi, tu peux ajouter deux dans l'intersection. Tu dois donc retirer deux dans les totaux de chacune des catégories, tu as alors 4 boules qui sont uniquement impaires et 1 boule qui est seulement un multiple de 5.
Pour plus d'information sur le diagramme de Venn, voici le lien vers une fiche de notre site pour t'aider :
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!😉
Anthony B.
Le 1 qui est dans B mais pas dans A :
il devrait y avoir 1 seul nombre qui est un multiple de 5 mais pas impair. Lequel?
Le 6 qui n'est ni dans A ni dans B:
il devrait y avoir 6 nombres qui ne sont ni impairs ni multiples de 5. Lesquels?
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!