Secondaire 5 • 3a
Vous l’avez très bien expliqué, merci énormément! Malheureusement, j’ai un Peu la misère avec la mise en évidence simple 😅 , je me mélange avec les fois et les moins , comment le faire ? J’ai fait ça pour le moment :
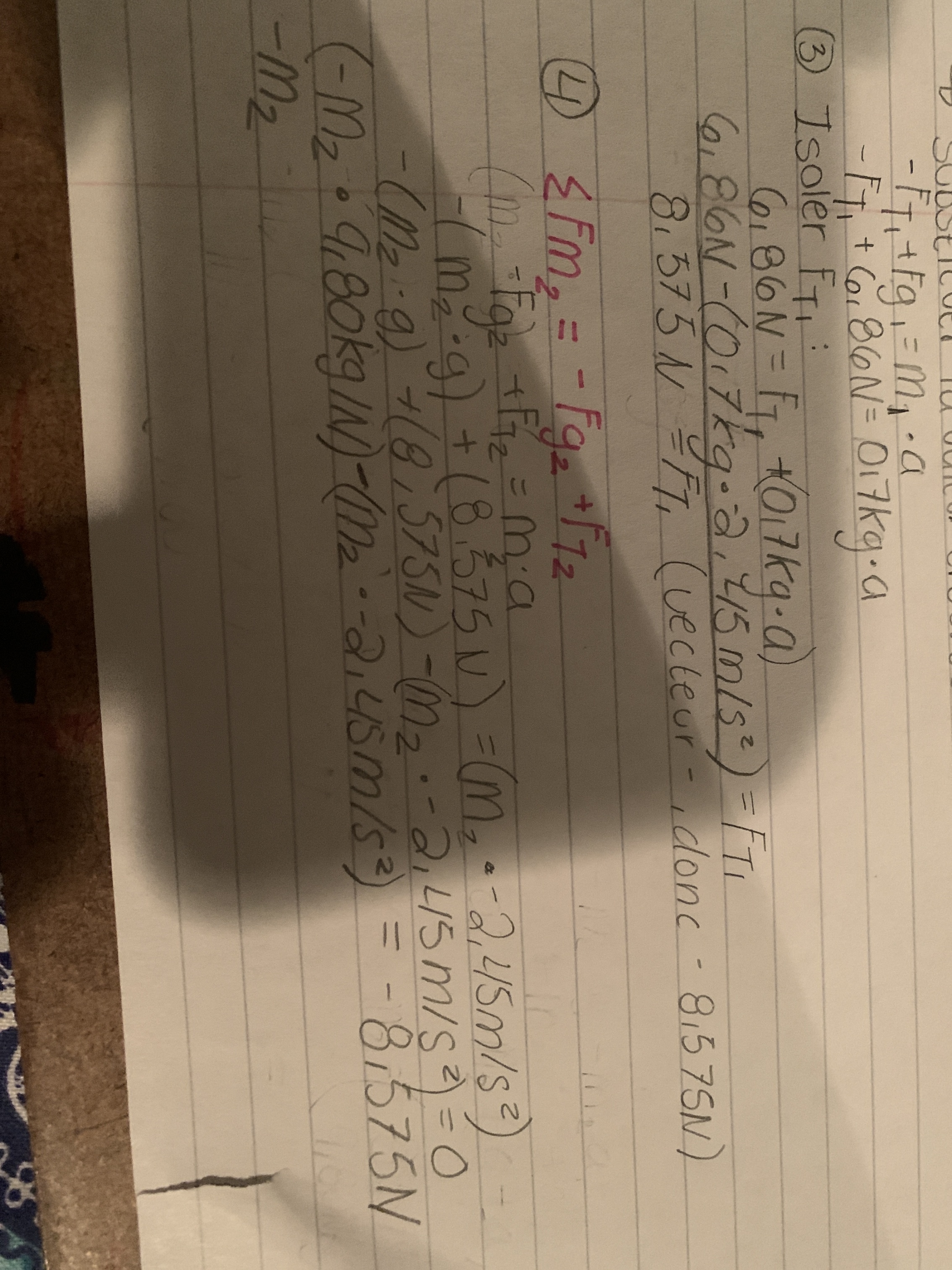






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Merci pour ta question!
L'autre réponse à ta question précédente est erronée. Comme je l'ai indiqué dans mes explications précédentes, il ne faut pas inclure la tension dans le calcul final puisque les tensions s'annulent dans ce problème. La somme des forces devient alors la suivante :
$$ \Sigma_F = F_{g1}+F_{g2} = m•a $$
Tu as établi que la masse de droite (m1) exerçait une force négative, alors gardons cela :
$$ \Sigma_F = m_1•(-g)+m_2•g = (m_1+m_2)•2,45 $$
$$ \Sigma_F = m_1•(-9,81)+m_2•(9,81) = (0,7 + m_{inconnue})•2,45 $$
On note m_inconnue ici car on ne sait pas laquelle des deux masses ne pèse pas 0,7.
$$ \Sigma_F = -9,81•m_1+9,81•m_2 = (0,7•2,45)+(m_{inconnue})•2,45 $$
On vient alors à un point où il faut décider si m1 ou m2 pèse 0,7 kg. Pour ce faire, on teste les deux valeurs et on s'assure que m2 > m1, comme tu l'as indiqué dans tes démarches. Essayons d'abord avec m1:
$$ \Sigma_F = -9,81•(0,7)+9,81•m_2 = (0,7•2,45)+m_2•2,45 $$
$$ -9,81•(0,7)+9,81•m_2 = (0,7•2,45)+m_2•2,45 $$
$$ -6,867+9,81•m_2 = 1,715+m_2•2,45 $$
Il faut alors isoler m2 et voir le résultat :
$$ 7,36m_2=8,582 $$
$$ m_2 ≈ 1,166\:kg $$
Par hasard, il s'agit de la bonne réponse car m_2>m_1
Voilà!
N'hésite pas si tu as d'autres questions!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!