Secondaire 5 • 2a
J’ai une question à propos des vecteurs.
Dans votre fiche, la section du calcul de l’orientation à partir des composantes semble avoir une erreur. (Je crois)
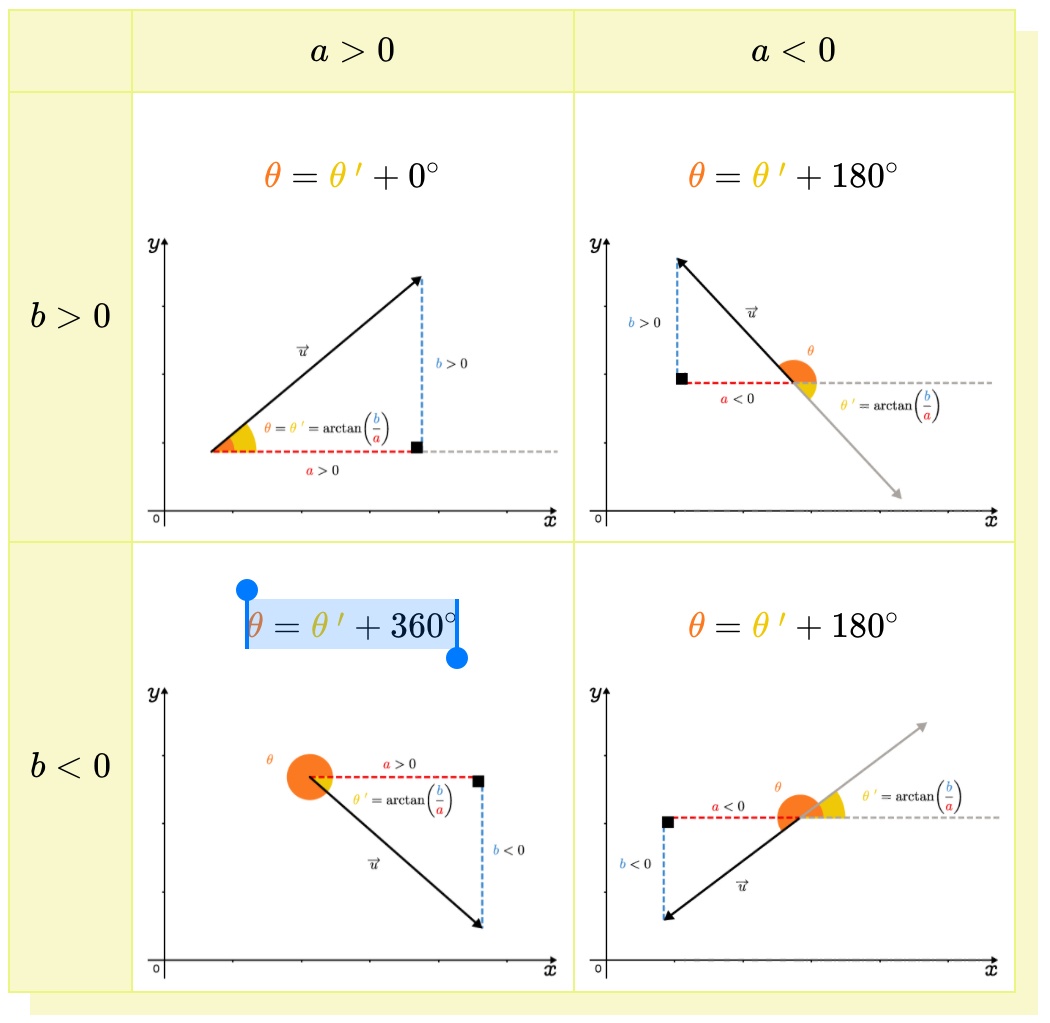
C’est écrit que lorsque la valeur de la composante a est positive et celle de la composante b est négative, il faut faire
θ = θ’+ 360^∘
Par contre, il n’est pas possible que la valeur de l’angle soit plus élevée que 360 degrés.
Alors ma question est: la formule n’est supposée être θ = 360^∘ - θ’ ?






Bonjour SaturneSarcelle7809,
Effectivement, un angle ne peut pas être plus grand que 360 degrés. Comme le mentionne AvocatTenace6777, l'angle θ' est négatif étant donné que b est négatif et a est positif. Par exemple, si a vaut 2 et b vaut -4, on utilise la formule pour calculer θ' et on obtient θ'=arctan(-2). À l'aide de la calculatrice, on obtient θ'=-63,43. Pour trouver θ, on ajoute 360 degrés, ce qui donne θ=296,57. Comme tu peux le constater, on obtient bel et bien un angle inférieur à 360 degrés.
C'est la même chose pour l'image en haut à droite, comme le mentionne AvocatTenace6777 dans son commentaire.
J'espère que ça va t'aider! :)
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Il n'y a pas d'erreur parce que θ’ = arctan(b/a) est négatif.
Pas d'erreur aussi pour le cas en haut à droite.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!