Zone d’entraide

RadisRose1197

Bonjour, je suis en calcul différentiel en j’aurais besoin d’aide pour évaluer les limites des problèmes ci-dessous.

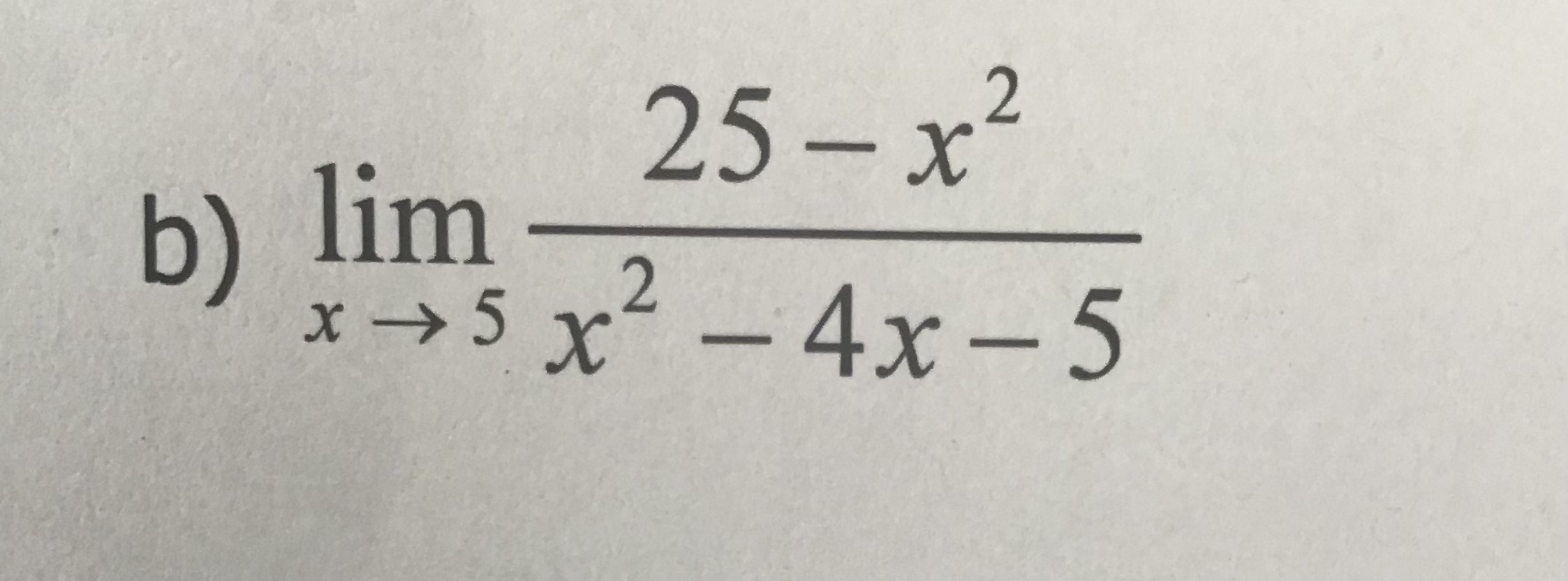
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

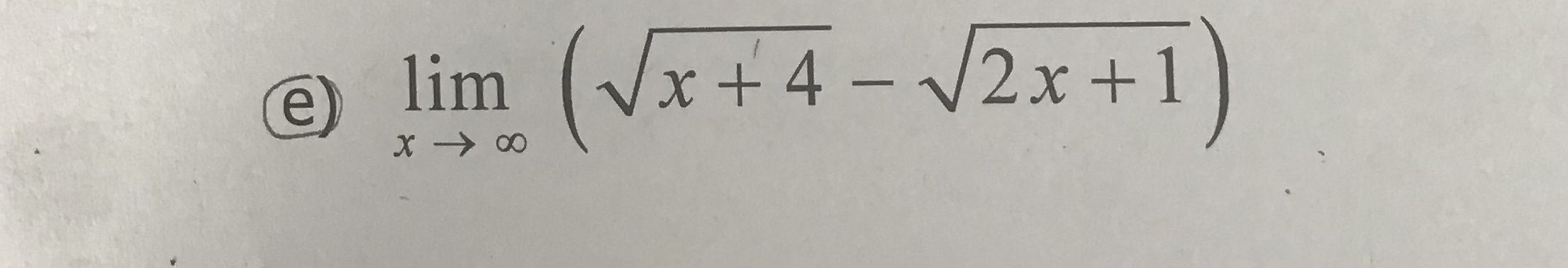
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

AvocatTenace6777

bonjour,

Alloprof répond seulement aux questions de niveau primaire et secondaire.

Cependant voici des indices:

b) décomposer en facteurs. Au numérateur, on a une différence de carrés. Au dénominateur on utilise la méthode produit-somme.

Rappel : 5-x=-x+5=-1(x-5).

a) et d) on multiplie le numérateur et le dénominateur par le conjugué.

Rappel: le conjugué de \( \sqrt{A}-B \) est \( \sqrt{A}+B \) et inversement.

e) on transforme l'expression ainsi:

\[ \sqrt{x+4}-\sqrt{2x+1} \]

\[ =\sqrt{x(1+\frac{4}{x})}-\sqrt{x(2+\frac{1}{x})} \]

\[ =\sqrt{x}\left (\sqrt{1+\frac{4}{x}}-\sqrt{2+\frac{1}{x}} \right ) \]

On termine en évaluant la limite.