Secondaire 5 • 2a
Bonjour!
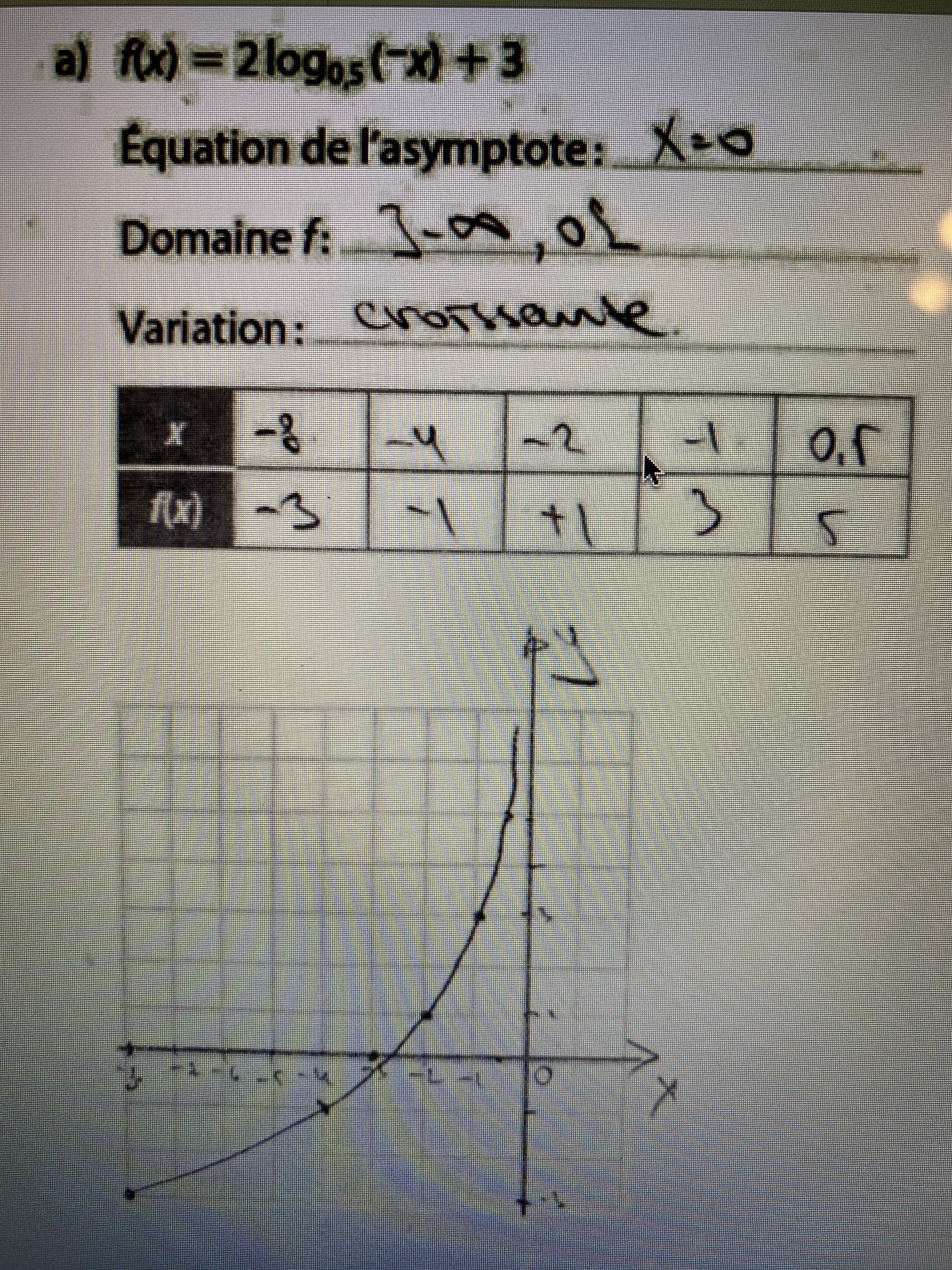
J’aimerais bien savoir comment on ferait pour trouver les résultats de la table de valeurs à partir de la fonction logarithmique en haut.
Je comprends comment on le ferait si le log était en base 10, comme la réponse est donnée par la calculatrice, mais si c’est une autre base, je ne comprends pas…
Merci beaucoup!






bonjour,
En choisissant bien les valeurs de x, on peut le faire mentalement ou presque !
Exemple:
\[ \log_{0.5}(8)= n \]
\[0.5^ n = 8\]
\[ (2^{-1})^{n}=2^3 \]
\[-n=3\]
\[n=-3\]
donc \[ \log_{0.5}(8)=-3 \]
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Pour répondre à ta question :
Tu as besoin de 2 choses :
1- Une calculatrice
2- Connaitre cette loi de log :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Le a dans cette image peut être remplacé par 10, car sur la calculatrice il n'y a que les log à base 10 (et à base e [que tu n'as surement pas vu encore]).
Ainsi,
$$\log_{2}{6}= \frac{\log_{10}{6}}{\log_{10}{2}}$$
Plus d'infos :
Bonne journée
KH
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!