Secondaire 4 • 2a
Bonsoir!
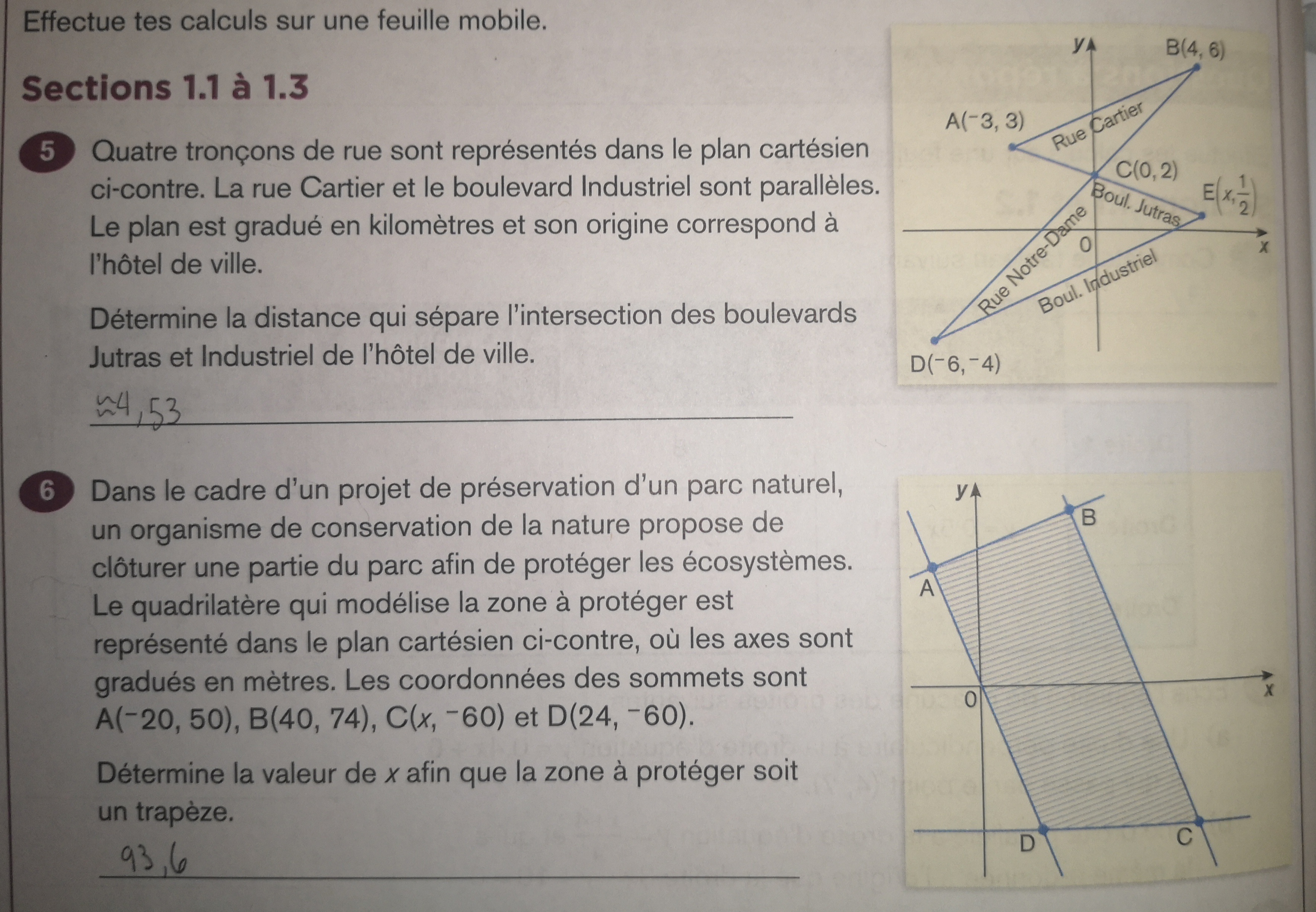
En fait, mon professeur m'a donné les réponses pour ces deux numéros... Mais à vrais dire je ne comprend pas vraiment comment me rendre à ces résolutions. J'ai essayé plusieurs fois mais je tombe toujours sur une autre réponse... Quelqu'un pourrais svp m'aider?






Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
bonjour,
Solution alternative:
Les segments AB et DE sont parallèles, donc ils ont la même pente.
\[ \frac{6-3}{4--3}=\frac{\frac{1}{2}--4}{x--6} \]
On résout pour x et on calcule la distance demandée.
Je vais t'aider avec le premier
Tu dois donc déterminer la distance de ( 0 , 0 ) l'origine où se trouve l'Hôtel de ville et E le point ( x , 1/2 ) sachant que AB et DE sont parallèles
Tu peux donc utiliser le rapport de similitude pour les composantes en x et en y de ces distances.
Pour AB la composante en x est 4 - (-3) = 7
et la composante en y est 6 - 3 = 3 .
Pour DE la composante en x est x - (-6) = x + 6
et la composante en y est (1/2) - (-4) = 9/2
Le rapport de similitude 7/3 = (x+6)/(9/2)
c'est-à-dire (7/3) (9/2) = (x+6)
ou 21/2 = x + 6
et x = (21 - 12)/2 = 9/2
Maintenant pour obtenir la distance de E à l'origine
on sait que la distance au carré est
( 1/2 - 0 )^2 + ( x - 0 )^2 = 1/4 + x^2 = 1/4 + 81/4 = 82/4
donc la distance est 4.53 (4.52769..)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!