Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Bonjour, pouvez vos m’aider svp ? Merci !!
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Bonjour FraiseExtraordinaire905,
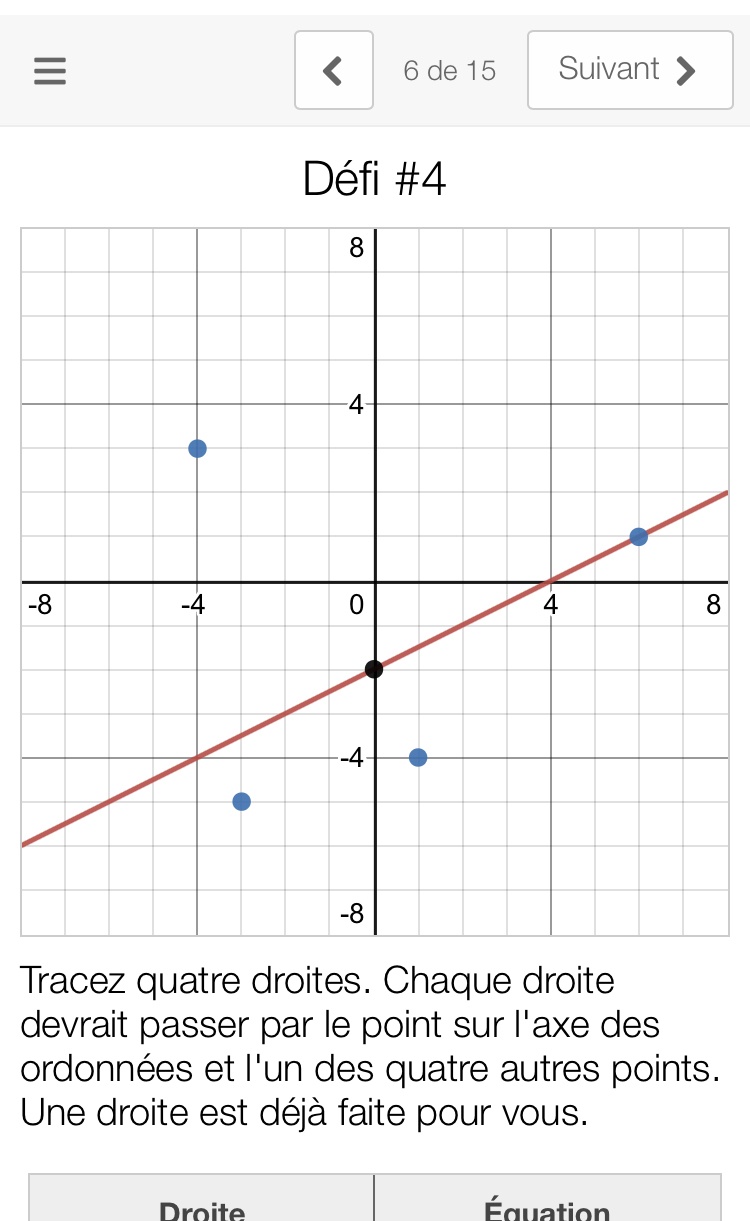
Afin de tracer les droites tu n’a qu’à relier le point noir à l’un des points bleu puis allonger la droite jusqu’au bout du graphique.
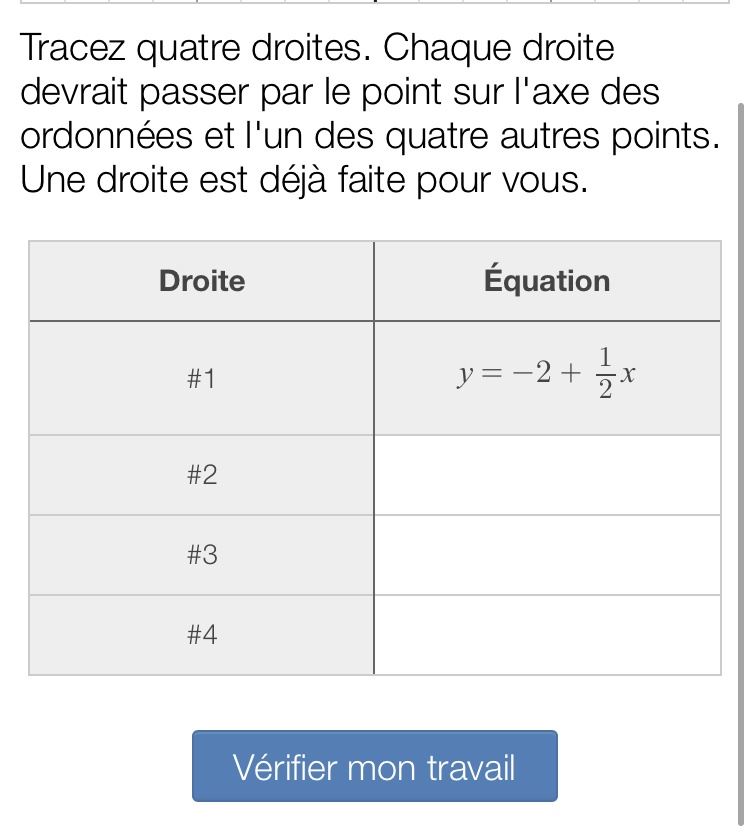
En ce qui concerne l’équation, nous savons que c’est une fonction de variation partielle, donc y=ax+b.
À partir de là, il faut trouver notre b, c’est notre ordonnée à l’origine, le point noir. Sur le graphique l’on constate que c’est -2. Notre équation ressemble maintenant à y=ax-2.
Pour trouver notre a, nous allons d’abord compter la hauteur du point bleu par rapport au point noir. Si l’on monte, le nombre sera positif, si l’on descend, il sera négatif. En prenant l’exemple, nous devons monter de trois afin de se rendre au point bleu. Ce sera notre numérateur. Le dénominateur pour lui, nous devons compter sur l’axe des x, sur la largeur, encore une fois à partir de notre point noir. Si nous allons vers la droite, le nombre sera positif, si nous allons vers la gauche, le nombre sera négatif. Dans le cas de l’exemple, nous nous déplaçons de 6 vers la droite. Nous avons maintenant une équation qui ressemble à y=3/6x-2.
Tout ce qui nous reste à faire c’est de réduire, le 3/6 devient 1/2. Et voilà, nous avons notre équation. y=1/2x-2
Tu dois tracer une droite passant par chacun des points en bleu (-4,3), (-3,-5) et (1, -4) et le point qui se situe sur l'axe des ordonnés (le point 0,-2). ensuite, tu calcules les règles de chaque affine.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!