Secondaire 3 • 2a
Bonjour,
S'il vous plaît, je veux une explication sur ces trois question.
1.
2.
3.
Merci.
Bonjour,
S'il vous plaît, je veux une explication sur ces trois question.
1.
2.
3.
Merci.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour,
Pour le numéro 1, tu dois avoir recours aux notions de recherche d'une règle d'une fonction affine. Celle-ci a la forme y = ax + b où a est le taux de variation et b est l'ordonnée à l'origine.
La règle de la fonction pour Jean-Christophe est déjà donnée, car 12$/h est le taux de variation et 10$ est l'ordonnée à l'origine.
Pour Pierre-Olivier, tu peux trouver le taux de variation grâce à la formule suivante.
$$ a = \dfrac{\Delta y}{\Delta x} = \dfrac{y_{2}-y_{1}}{x_{2}-x_{1}} $$
Tu peux ensuite reprendre y = ax + b en y remplaçant une cordonnée (x, y), puis le a précédemment trouvé afin d'obtenir la valeur de b. Tu auras ainsi l'équation.
La recherche de la règle d'une fonction affine:
Pour le A), on demande si b est pareil pour les deux.
Pour le B), tu dois en premier trouver le nombre d'heures à travailler sachant que le terrain a une superficie de 1 800 m^2 et que tondre 250 m^2 prend une demi-heure.
$$ \frac{x}{1 800 m^2} = \frac{10,5 h }{250 m^2} $$
La résolution de situations directement ou inversement proportionnelles:
Lorsque x est le même, est-ce que y est pareil dans les deux cas? Calcule pour chaque équation.
Pour C), pour quel x les y seront les mêmes ? Tu dois poser les équations y1=y2 puis isoler x pour trouver sa valeur.
La résolution de systèmes d'équations linéaires:
Pour le deuxième problème, tu dois encore trouver la règle.
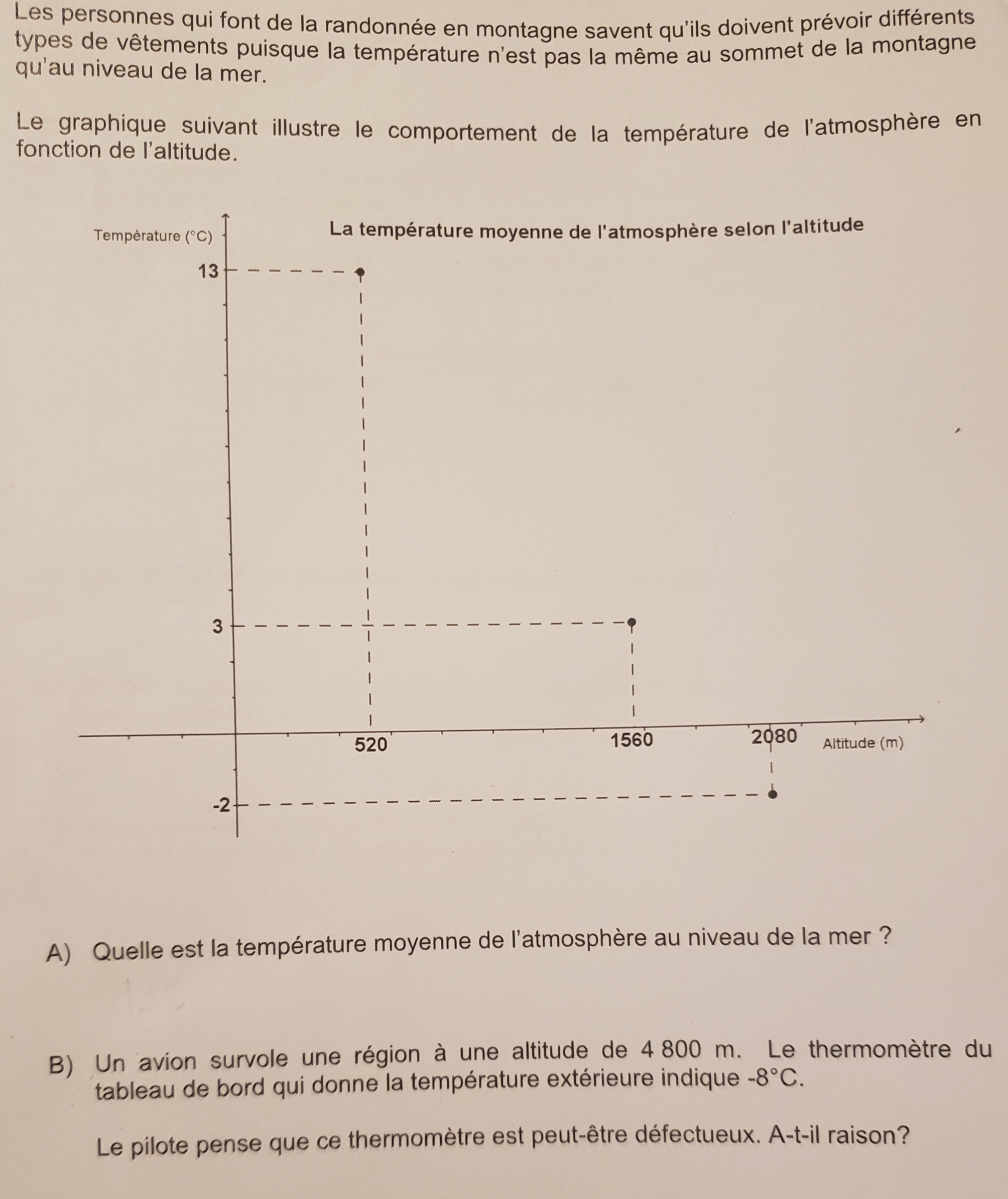
Tu as les trois coordonnées (520, 13), (1560, 3) et (2080, -3). En utilisant deux d'entre elles, tu peux trouver le taux de variation.
Ensuite, choisis une coordonnée, puis remplace le x et y dans la formule y = ax + b. Ayant les valeurs de y, a et x, tu peux trouver b et avoir ainsi la règle complète.
On te demande en A) de trouver la valeur y pour le x, étant l'altitude au niveau de la mer. Tu remplaces le x dans l'équation pour avoir y.
En B), on veut savoir s'il est vrai que si x = 4 800 m, le y sera -8°C.
Pour le troisième problème, tu dois trouver la règle selon les mêmes techniques que les deux derniers numéros.
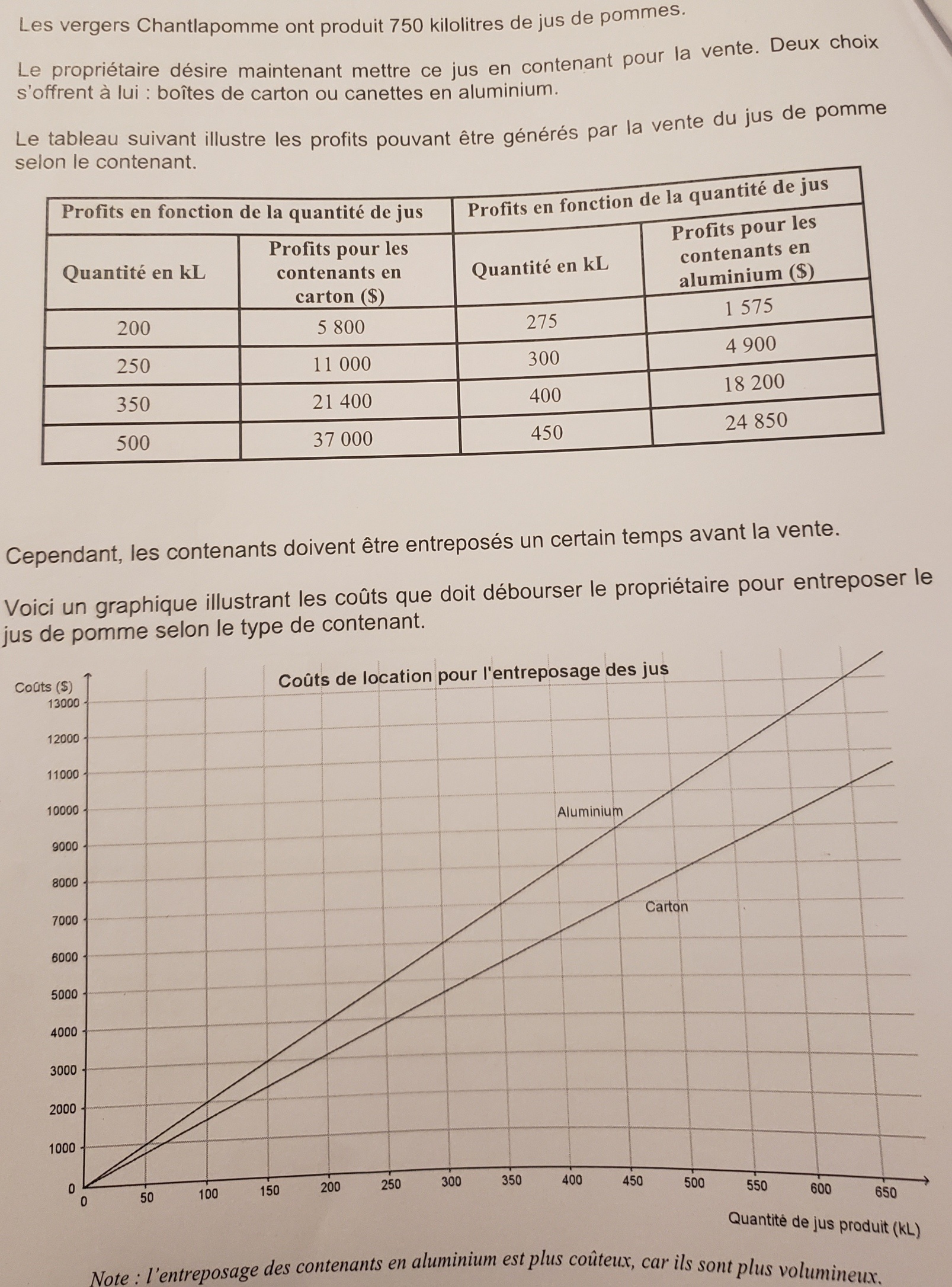
1) Une pour le profit pour le contenant en carton.
2) Une pour le profit pour le contenant en aluminium.
Le x est la quantité de jus et le y est le profit.
3) Une pour le coût d'entreposage pour le contenant en carton.
4) Une pour le coût d'entreposage pour le contenant en aluminium.
a4) Une pour le coût d'entreposage pour le contenant en
Le x est la quantité de jus et y est le coût.
Cette fois tu as un graphique, non un tableau, mais tu as quand même des coordonnées très claires!
Ensuite, nous savons que x = 750 kL de jus.
Ainsi, quel sera le coût d'entreposage selon le matériel? Quel sera le profit? Tu as x et tu cherches y. Tu peux enfin soustraire (le profit - le coût) pour savoir lequel génère le plus d'argent!
N'hésite pas si tu as d'autres questions!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!