Secondaire 3 • 2a
Salut!
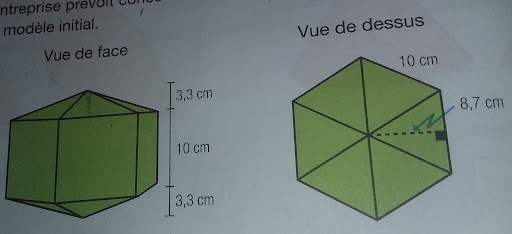
Comment je suis sensé trouver le volume de cette figure????
Est ce qu'il me faudrait l'apothème de la base de la pyramide? Parce que le volume d'une pyramide c'est ((aire de la base x hauteur)/3) et que l'aire de la base de cette pyramide c'est ((mesure d'un côté x apothème x nombre de côtés)/2).
Merci!






Explication d'un(e) pro de la Zone d'entraide
Tu peux faire confiance à cette explication, car elle est donnée par une personne identifiée comme étant fiable par Alloprof.
Salut ElfeAgile,
simplement pour te signifier que j'ai mis à jour mon message précédent (au cas où tu n'aies pas eu l'occasion de voir la modification).
Bonne journée !
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Salut !
EDIT : J'ai construit la figure dans Géogébra, et il semble que la mesure de 8,7 cm soit la mesure de l'apothème de la base, c'est-à-dire ce que tu as besoin pour calculer le volume (et non la mesure de l'apothème de la pyramide). Il y a parfois des erreurs dans les livres, donc je crois que tu devrais consulter ton enseignant(e) pour en avoir le cœur net.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
(clique sur l'image pour agrandir)
Néanmoins, voici la réponse que j'avais donnée initialement :
En effet, tu pourrais calculer le volume de ce solide en effectuant la somme des volumes des deux pyramides droites à base hexagonale (en haut et en bas) et du prisme droit à base hexagonale (au centre). Dans les deux calculs des volumes, tu dois connaître l'aire de l'hexagone (la base de la pyramide et la base du prisme).
Heureusement, l'apothème de la pyramide (8,7 cm), la hauteur de la pyramide (3,3 cm) et l'apothème de la base (ce que tu cherches) forment un triangle rectangle.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
(source de l'image : https://scientificsentence.net/Equations/Maths2/revisions2/index.php?key=yes&Integer=aires_volumes_divers)
Tu peux donc calculer l'apothème avec la relation de Pythagore :
\[3,\!3^2 + \left(a_{\text{base}}\right)^2 = 8,\!7^2\]
\[\dots\]
Bon succès !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!