Zone d’entraide

MerleLibre9942

Bonjour,

J'ai de la difficulté avec la compréhension de mes formules.

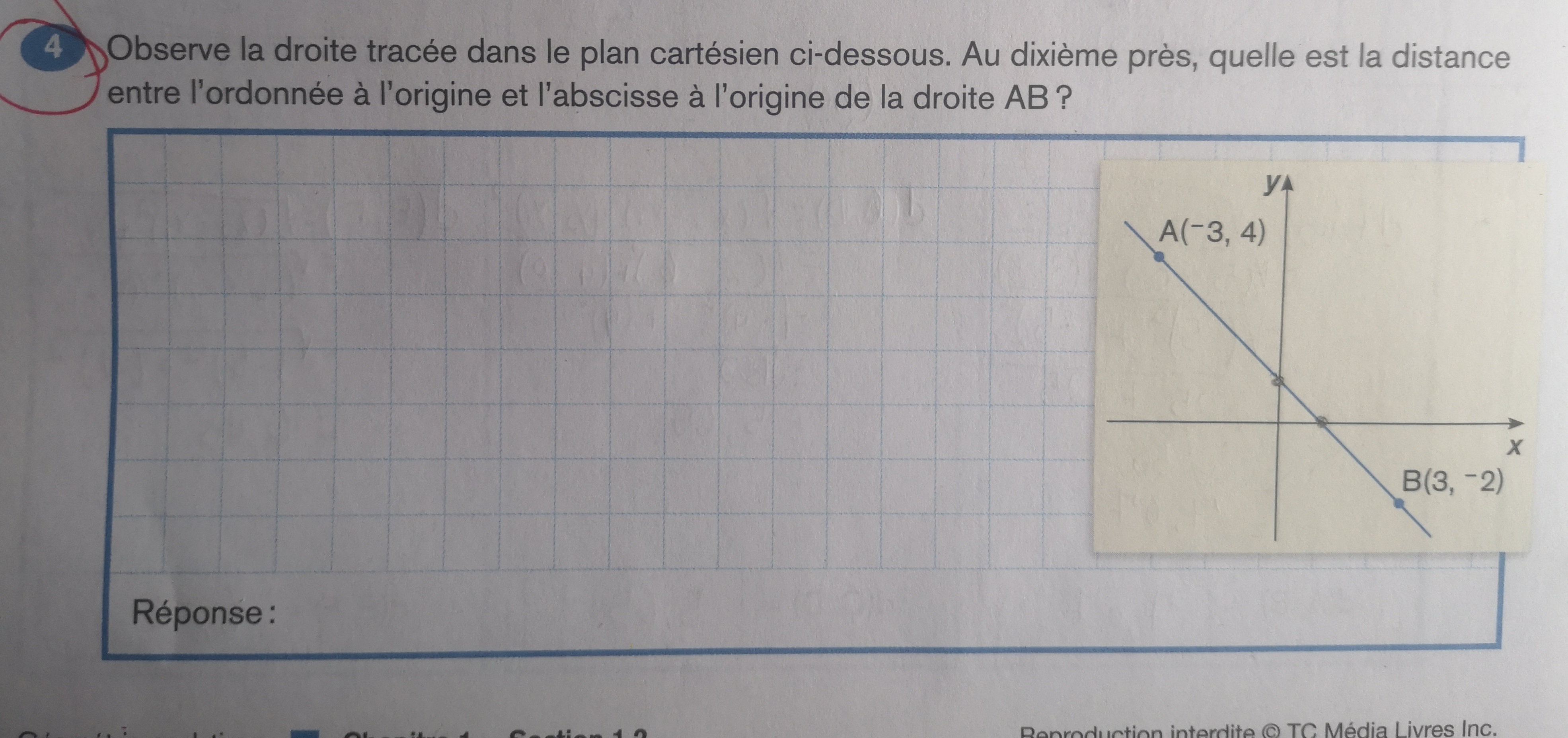
Avec c'est trois numéros, quel sont mes étapes pour trouvé les résolutions?

.. Quelqu'un pourrait s'il-vous-plaît m'aider? Désolé 😅

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

LoupAdorable2932

Demande à un de tes parents de t’aider

Kevin H

Bonjour,

Les trois questions on en commun la distance entre 2 points.

La distance entre le point $A$ et le point $B$ correspond à la mesure du segment $\overline{AB}$.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$$d(A,B)=m\overline{AB}$$

$(x_1,y_1)$ sont les coordonnées d'une des deux extrémités du segment et $(x_2,y_2)$ sont les coordonnées de l'autre extrémité du segment. Tu peux avoir $A:(x_1,y_1)$ et $B:(x_2,y_2)$, ou l'inverse : $B:(x_1,y_1)$ et $A:(x_2,y_2)$. Cela est possible, car la distance entre $A$ et $B$ est la même que la distance entre $B$ et $A$.

Ainsi c'est toi qui décides quelle extrémité a pour coordonnées $(x_1,y_1)$ et laquelle a $(x_2,y_2)$.

(L'important est de ne pas se mélanger et d'intervertir les abscisses et ordonnées de tes points. En effet, écrire cela serait faux : $A(x_1,y_2)$ et $B(x_2,y_1)$.

La « formule » de la distance entre deux points peut s'expliquer avec la relation de Pythagore (tu formes un triangle rectangle et calcules les accroissements)

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

$d(A,B)=\sqrt{{(x2-x1)}^2+{(y2-y1)}^2}$

Je t'invite à cliquer sur ce lien pour :

Alloprof aide aux devoirs | Alloprof

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/math-la-distance-entre-deux-points-m1311

Grâce à ses services d’accompagnement gratuits et stimulants, Alloprof engage les élèves et leurs parents dans la réussite éducative.

Bonne journée !