Secondaire 5 • 3a
Bonjour,
En trigonométrie, pour l'analyse de la fonction, est-ce qu'il faut toujours partir du point de référence dit point de départ du premier cycle?
Par exemple, dans cet exercice, est-ce qu'il serait faux d'affirmer que c'est positif de [-2,5pie + n2pie , -1,5 pie + n2pie ]?
Ainsi, de suite, en négatif, pouvons-nous ne pas dire que celle l'est de [-1,5pie + n2pie, -2pie + n2pie]?
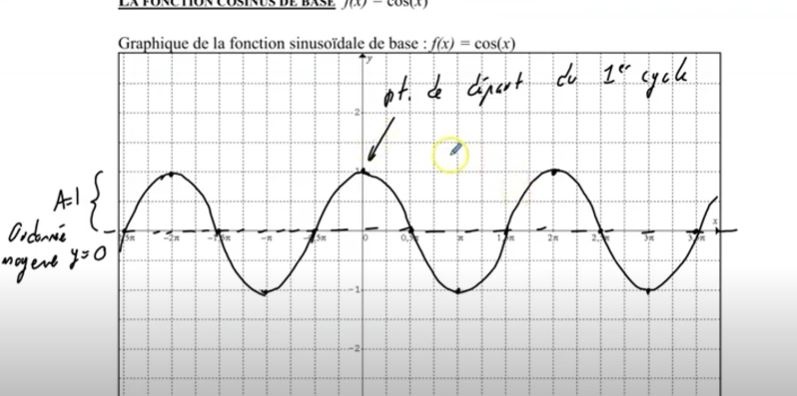
Fonction cosinus de base.
Merci et bonne journée! :)






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour Or Autonome!
Merci de faire appel à nos services 😉
Pour t'aider à déterminer les intervalles où une fonction sinusoïdale est positive ou négative, tu peux consulter la fiche explicative suivante qui montre des exemples des intervalles à établir:
J'espère que cela t'aidera!
Salut!
On peut choisir le cycle que l'on veut.
« positif de [-2,5pie + n2pie , -1,5 pie + n2pie ] ? »
On peut le dire, c'est VRAI.
« négatif, pouvons-nous ne pas dire que celle l'est de [-1,5pie + n2pie, -2pie + n2pie]? »
C'est FAUX. (erreur dans la borne supérieure)
On pourrait dire négatif sur [-1,5pi + n2pi, -0,5pi + n2pi].
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!