Secondaire 4 • 2a
Bonjour!
Alors en fait je suis scolarisé à la maison depuis début janvier donc je ne peu pas vraiment contacter mes professeurs pour des questions instantané.
Pouvez-vous m'aider avec ce numéro? Je ne sais pas vraiment par où commencé. Je me casse la tête haha mais je ne comprend pas.






Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Bonjour Scorpion Iota
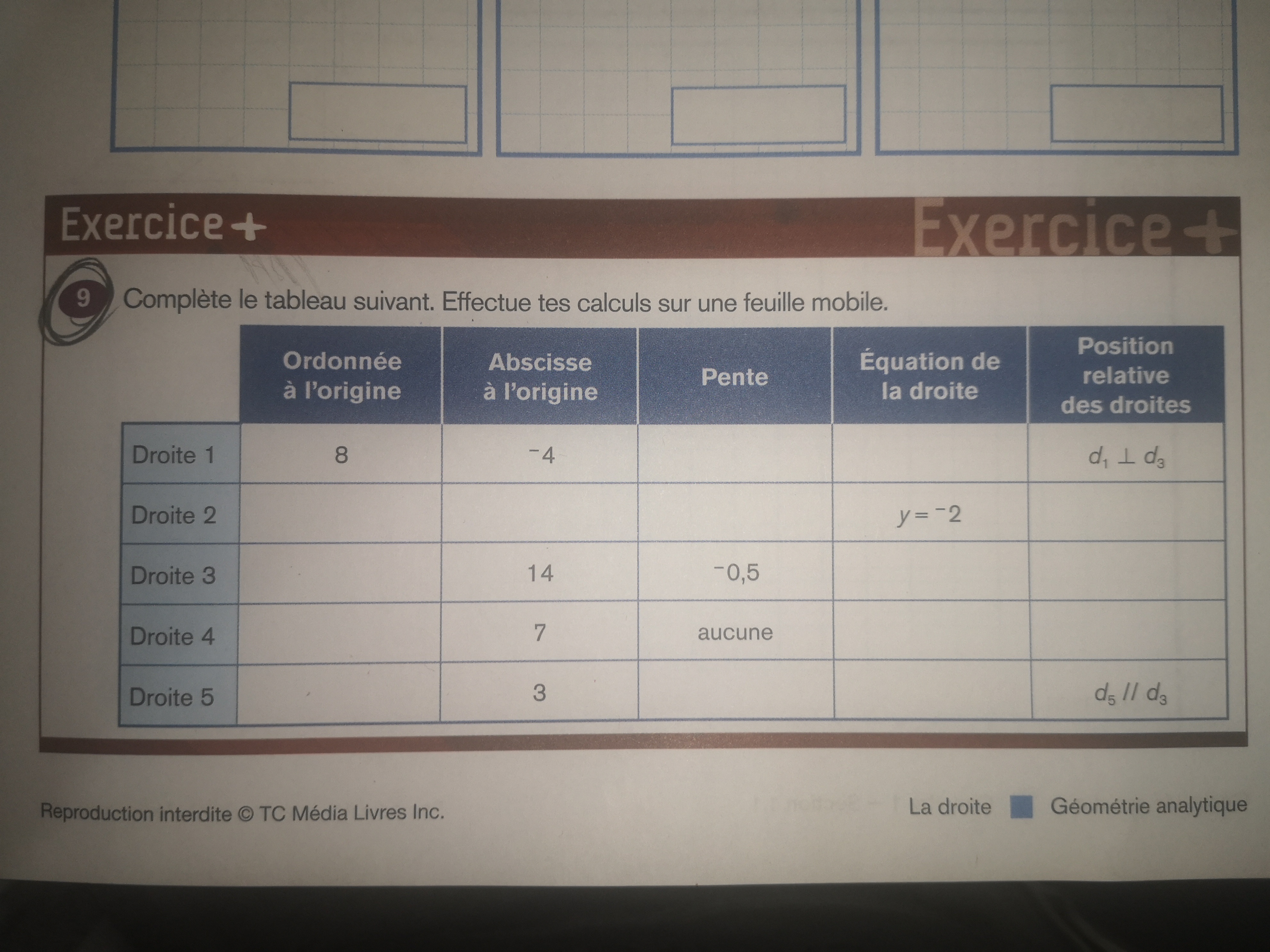
Il s'agit ici d'un numéro sur les droites !
Ils te donnent certaines informations et tu dois compléter. Je te recommande de prendre une feuille et de tracer une esquisse de la droite avec l'info que tu connais ( par exemple, pour la droite #1, tu sais que l’ordonnée à l'origine est de 8 et que l’abscisse à l'origine est de -4)
Tu as donc 2 couples (0,8) (-4,0), tu peux donc trouver la pente ;) . comme ton équation est de forme y=ax+b, en ayant la pente (a) et l'ordonnée à l'origine , tu as ton équation !
Pour la droite#2 ; ton équation est encore y=ax+b. on te donne la pente et l’abscisse à l'origine, tu peux alors isoler pour avoir b (ordonnée à l'origine)
Les autres numéros se font de la même manière. Tu dois simplement savoir les caractéristiques de deux pentes parallèles et/ou perpendiculaires.
Je te joins une fiche Alloprof qui explique ces caractéristiques ;)
Finalement, il ne te restera qu'à écrire la position relative des droites. Si tu traces tes droites et que tu regardes les pentes ça va t'aider à trouver les réponses ;)
Essaye donc de remplir une case à la fois et de compléter tranquillement le tableau !
n'hésite pas si tu as d'autres questions
VC
L'ordonnée à l'origine 8 c'est le point (0,8)
alors que l'abscisse à l'origine -4 c'est le point (-4,0)
Avec les informations données dans le tableau, tu devrais pouvoir compléter les blancs.
(le symbole // t'indique que les droites sont parallèles)
Aussi consulte la page suivante, ça devrait t'aider
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!